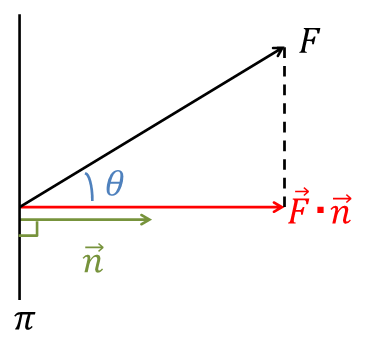石井俊全「一般相対性理論を一歩一歩数式で理解する」ベレ出版 の読後行間補充メモ
§1 ニュートンの重力場方程式
p126 質点 \(A_i\) と\(B\)
p126 ニュートンの重力ポテンシャル \(\phi(\vec{x})\)
質量密度 \(\rho\left[\frac{kg}{m^3}\right]\) に体積 \([m^3]\) を乗じたものは、質量 \([kg]\)。
質量密度が位置 \(\vec{y}\) によって異なる場合、質量密度は、\(\vec{y}\) の変数として\(\rho(\vec{y})\) と表される。この \(\rho(\vec{x})\) と各位置における微小体積と乗じたものを \(V\) 内で合計したものは、領域 \(V\) 内の合計質量\[\int_V \rho(\vec{y})~d\vec{y}\]となる。
p127 重力ポテンシャル \(\phi(\vec{x})\)
位置 \(\vec{x}\) における単位質量あたりの重力による位置エネルギー。
単位は、 \begin{eqnarray}\left[\frac{J}{kg}\right]&=&\left[\frac{N\cdot m}{kg}\right]\nonumber\\ &=&\left[\frac{kg\cdot\frac{m}{s^2}\cdot m}{kg}\right]\nonumber\\&=&\left[\frac{m^2}{s^2}\right]\nonumber\end{eqnarray}
p127 \(\mathrm{grad}\frac{1}{|\vec{y}-\vec{x}|}\)
勾配 \(\mathrm{grad}\) の定義(p36)より、\(x\) 座標軸\[\left(\begin{array}{x}x_1\\x_2\\x_3\end{array}\right)\] での \(\frac{1}{|\vec{y}-\vec{x}|}\) の勾配は、\[\mathrm{grad}\frac{1}{|\vec{y}-\vec{x}|}=\left(\begin{array}{x}\frac{\partial}{\partial x_1}\frac{1}{|\vec{y}-\vec{x}|}\\ \frac{\partial}{\partial x_2}\frac{1}{|\vec{y}-\vec{x}|}\\ \frac{\partial}{\partial x_3}\frac{1}{|\vec{y}-\vec{x}|}\end{array}\right)\]であるところ、1行目は、第1章 数学の準備 [p110 赤字部分(公式1.35の \(\mathrm{grad} f\) を計算するときの要領]のとおり、\begin{eqnarray}\frac{\partial}{\partial x_1}\frac{1}{|\vec{y}-\vec{x}|}&=&\frac{y_1-x_1}{|\vec{y}-\vec{x}|^3}\nonumber\end{eqnarray}となる。
2行目も、同様に計算して、以下のようになる。\begin{eqnarray}\frac{\partial}{\partial x_2}\frac{1}{|\vec{y}-\vec{x}|}&=&\frac{y_2-x_2}{|\vec{y}-\vec{x}|^3}\nonumber\end{eqnarray}3行目も、同様に、\begin{eqnarray}\frac{\partial}{\partial x_3}\frac{1}{|\vec{y}-\vec{x}|}&=&\frac{y_3-x_3}{|\vec{y}-\vec{x}|^3}\nonumber\end{eqnarray}となるので、これら3つの計算結果をまとめると、与式は、\begin{eqnarray}\mathrm{grad}\frac{1}{|\vec{y}-\vec{x}|}&=&\left(\begin{array}{x}\frac{y_1-x_1}{|\vec{y}-\vec{x}|^3}\\ \frac{y_2-x_2}{|\vec{y}-\vec{x}|^3}\\\frac{y_3-x_3}{|\vec{y}-\vec{x}|^3}\end{array}\right)\nonumber\\&=&\frac{1}{|\vec{y}-\vec{x}|^3}\left(\begin{array}{x}y_1-x_1\\y_2-x_2\\y_3-x_3\end{array}\right)\nonumber\\&=&\frac{1}{|\vec{y}-\vec{x}|^3}(\vec{y}-\vec{x})\nonumber\\&=&\frac{\vec{y}-\vec{x}}{|\vec{y}-\vec{x}|^3}\nonumber\end{eqnarray}となる。
p127 重力ポテンシャルの勾配 \(\bigtriangledown\phi(\vec{x})\)
位置 \(\vec{x}\)での重力場(のマイナス)。
単位は、\[\frac{\partial}{\partial \vec{x}}\left[\frac{m^2}{s^2}\right]=\left[\frac{m}{s^2}\right]\]
p127 重力ポテンシャルのラプラシアン \(\Delta\phi(\vec{x})\)
単位は、\[\frac{\partial^2}{\partial \vec{x}^2}\left[\frac{m^2}{s^2}\right]=\left[\frac{1}{s^2}\right]\]
§2 応力テンソル
p132 応力 \(T,~S\) の比較
応力 \(\vec{T},~\vec{S}\) は、単位面積あたりの力 \(\left[\frac{N}{m^2}\right]\) を指しているので、応力\(\vec{T}\) を認識する断面の面積を \(P_T\) 、応力\(\vec{S}\) を認識する断面の面積を \(P_S\) とすると、\[P_S~\cos\theta=P_T\]の関係があるから、応力に対応断面積を乗じた力どうしの比較では、\begin{eqnarray}|\vec{T}|\cos\theta \times P_T&=&|\vec{S}|\times P_S\nonumber\\ |\vec{T}|\cos\theta \times P_S\cos\theta&=&|\vec{S}|\times P_S\nonumber\\|\vec{T}|\cos^2\theta&=&|\vec{S}|\nonumber\end{eqnarray}となる。
p133 \(\tau_{yx}\neq\tau_{yy}\neq\tau_{yz}\)
- \(\tau_{yx}\) … \(x\) 軸に垂直な微小面の左側にある物質が微小面を \(y\) 軸方向にずらそうとする剪断力
- \(\tau_{yy}\) … \(y\) 軸に垂直な微小面の手前側にある物質が微小面を \(y\) 軸方向に押す力
- \(\tau_{yz}\) … \(z\) 軸に垂直な微小面の下側にある物質が微小面を \(y\) 軸方向にずらそうとする剪断力
p134 \(n_z=\cos\theta\)
\begin{eqnarray}\vec{n}\cdot\vec{e_z}&=&|\vec{n}||\vec{e_z}|\cos\theta\nonumber\\&=&1\times 1 \times \cos\theta\nonumber\\&=&\cos\theta\nonumber\end{eqnarray}他方で、\begin{eqnarray}\vec{n}\cdot\vec{e_z}&=&\left(\begin{array}{x}n_x\\n_y\\n_z\end{array}\right)\cdot\left(\begin{array}{x}0\\0\\1\end{array}\right)\nonumber\\&=&n_x\times 0+n_y\times 0+n_z\times 1\nonumber\\&=&n_z\nonumber\end{eqnarray}従って、\[n_z=\cos\theta\]
p135 平面 \(\pi\) の圧縮応力の大きさ \(\vec{F}\cdot\vec{n}\)
p136 力のモーメント \(T\)
力を \(F[N]\)、回転半径を \(r[m]\) とすると、
\[T=Fr\]
単位は、\([N\cdot m]\)
p137 慣性モーメント \(I\)
回転体の回転のし難さ(慣性モーメント)\(I\) は、回転体の質量を \(M[kg]\)、半径を \(r[m]\) とすると、
\[I=kMr^2\]
単位は、\([kg\cdot m^2]\)
p137 角加速度 \(\ddot{\theta}\)
- 角度 \(\theta~~~[rad]\)
- 角速度 \(\dot{\theta}=\frac{d}{dt}\theta~~~[\frac{rad}{s}]\)
- 角加速度 \(\ddot{\theta}=\frac{d^2}{dt^2}\theta~~~[\frac{rad}{s^2}]\)
p137 回転の運動方程式 \(I\ddot{\theta}=T\)
直線の運動方程式は、\[ma=F\]単位は、\begin{eqnarray}[kg]\times \left[\frac{m}{s^2}\right]&=&\left[\frac{m\cdot kg}{s^2}\right]\nonumber\\&=&[N]\nonumber\end{eqnarray}
これに対し、回転の運動方程式は、慣性モーメントを \(I\)、角加速度を\(\ddot{\theta}\)、トルクを \(T\) とすると、\[I\ddot{\theta}=T\]単位は、\begin{eqnarray}[kg\cdot m^2]\times\left[\frac{rad}{s^2}\right]&=&\left[\frac{m\cdot kg}{s^2}\cdot m\cdot(rad)\right]\nonumber\\&=&[N\cdot m\cdot(rad)]\nonumber\\&=&[N\cdot m]\nonumber\end{eqnarray}
*角度\(rad\)は、弧の長さ(\(m\))と半径の長さ(\(m\))の比 (\(\frac{m}{m}=1\) 。無次元量)のため、省略記載。
p138 面積力と体積あたりの力
ガウスの発散定理より、\(x\) 軸に垂直な微小面に対する応力 \(\tau_x\) について、\[\int_S\tau_x\cdot \vec{n}~dS=\int_V\mathrm{div}\tau_x~dS\] 他の成分についても、同様の等式が成立するので、p138の6~7行目の等式が成立する。
p138 アインシュタインの縮約記法による書換え
- \(x,~y,~z\) を\(x\) 系座標の趣旨で \(x_1,~x_2~x_3\)
- 単位法線ベクトルを \(\vec{n}=\left( \begin{array}{x}n_1\\n_2\\n_3 \end{array}\right)\)
- \(\tau=\left(\begin{array}{x}\tau_{11}&&\tau_{12}&&\tau_{13}\\ \tau_{21}&&\tau_{22}&&\tau_{23}\\ \tau_{31}&&\tau_{32}&&\tau_{33}\end{array}\right)\)
と表記すると、\(\tau\)行列1行目の \[\vec{\tau_1}=(\tau_{11},~\tau_{12},~\tau_{13})\] と単位法線ベクトル \(\vec{n}\) の内積は、
\begin{eqnarray}\tau_1\cdot \vec{n}&=&(\tau_{11},~\tau_{12},~\tau_{13})\left(\begin{array}{x}n_1\\n_2\\n_3\end{array}\right)\nonumber\\&=&\tau_{11}n_1+\tau_{12}n_2+\tau_{13}n_3\nonumber\\&=&\tau_{1j}~n_j~\nonumber\end{eqnarray}と縮約記法で表記できる (走る添え字 \(j\) は、数値1, 2, 3 をとるものとする)。
\(\tau\)行列2行目の \(\vec{\tau_2}\) と \(\vec{n}\) との内積も、同様に、\[\tau_2\cdot\vec{n}=\tau_{2j}~n_j\]となり、\(\tau\)行列3行目の \(\vec{\tau_3}\) と \(\vec{n}\) との内積も、同様に、\[\tau_3\cdot\vec{n}=\tau_{3j}~n_j\]となる。
これら3式を、縮約記法でまとめ表記すると、\[\left.\begin{array}{x}\tau_{1j}~n_j\\ \tau_{2j}~n_j\\ \tau_{3j}~n_j\end{array}\right\}=\tau_{ij}~n_j\]と表される(止まっている添え字 \(i\) は、数値1, 2, 3 をとるものとする)。
すなわち、\begin{eqnarray}\left(\begin{array}{x}\tau_x\cdot\vec{n}\\ \tau_y\cdot\vec{n}\\ \tau_z\cdot\vec{n}\end{array}\right)&=&\left(\begin{array}{x}\tau_1\cdot\vec{n}\\ \tau_2\cdot\vec{n}\\ \tau_3\cdot\vec{n}\end{array}\right)\nonumber\\&=&\tau_{ij}~n_j\nonumber\end{eqnarray}よって、p138 の6~7行目の式の左辺は、以下のとおり、同頁下から2行目の式の左辺に書換え表記できる。\begin{eqnarray}\left(\begin{array}{x}\int_S\tau_x\cdot\vec{n}~dS\\ \int_S\tau_y\cdot\vec{n}~dS\\ \int_S\tau_z\cdot\vec{n}~dS\end{array}\right)&=&\int_S\tau_{ij}~n_j~dS\nonumber\end{eqnarray}
他方、右辺については、\(\mathrm{div}~\tau_x\)を例にとると、\begin{eqnarray}\mathrm{div}~\vec{\tau_x}&=&\mathrm{div}~\vec{\tau_{x_1}}\nonumber\\&=&\left(\begin{array}{x}\frac{\partial}{\partial x_1}\\ \frac{\partial}{\partial x_2}\\ \frac{\partial}{\partial x_3}\end{array}\right)\cdot(\tau_{11},~\tau_{12},~\tau_{13})\nonumber\\&=&\frac{\partial \tau_{11}}{\partial x_1}+\frac{\partial \tau_{12}}{\partial x_2}+\frac{\partial \tau_{12}}{\partial x_3}\nonumber\\&=&\frac{\partial \tau_{1j}}{\partial x_j}\nonumber\end{eqnarray}と縮約記法で表記できる (走る添え字 \(j\) は、数値1, 2, 3 をとるものとする)。よって、同様に、\[\mathrm{div}~\vec{\tau_y}=\frac{\partial \tau_{2j}}{\partial x_j}\]\[\mathrm{div}~\vec{\tau_z}=\frac{\partial \tau_{3j}}{\partial x_j}\]
と表記できるので、これら3式を縮約記法でまとめ表記すると、\[\left.\begin{array}{x}\mathrm{div}~\vec{\tau_x}\\ \mathrm{div}~\vec{\tau_y}\\ \mathrm{div}~\vec{\tau_z} \end{array}\right\}=\frac{\partial \tau_{ij}}{\partial x_j}\]と表される(止まっている添え字 \(i\) は、数値1, 2, 3 をとるものとする)。
よって、p138 の6~7行目の式の右辺は、以下のとおり、同頁下から2行目の式の右辺に書換え表記できる。\begin{eqnarray}\left(\begin{array}{x}\int_V\mathrm{div}~\tau_x ~dV\\ \int_V\mathrm{div}~\tau_y ~dV\\ \int_V\mathrm{div}~\tau_z ~dV\end{array}\right)&=&\int_V\frac{\partial \tau_{ij}}{\partial x_j}~dV\nonumber\end{eqnarray}従って、p138 の下から2行目の式が成立する。
p140 平行六面体の体積
\[h\Delta S=\vec{v}\cdot\vec{n}\Delta S\]
p142 流体が持つ運動量
\(\rho\vec{v}\cdot \vec{n}\) はスカラー量なので、ベクトルの各要素と乗ずることができ、
\begin{eqnarray}(\rho\vec{v}\cdot \vec{n})\vec{v}&=&\rho\vec{v}\cdot\vec{n}\left(\begin{array}{x}v_x\\v_y\\v_z\end{array}\right)\nonumber\\&=&\left(\begin{array}{x}\rho v_x\vec{v}\cdot \vec{n}\\ \rho v_y\vec{v}\cdot \vec{n}\\ \rho v_z\vec{v}\cdot \vec{n}\end{array}\right)\nonumber\end{eqnarray}
p142 式2.04
各要素にガウスの発散定理を適用している。
例えば、括弧内の第1要素について、\[\vec{A}=\rho v_x\vec{v}\]として、\begin{eqnarray}\int_S\rho v_x\vec{v}\cdot\vec{n}~dS&=&\int_S \vec{A}\cdot\vec{n}~dS\nonumber\\&=&\int_V \mathrm{div}\vec{A}~dV\nonumber\\&=&\int_V \mathrm{div}(\rho v_x\vec{v})~dV\nonumber\end{eqnarray}第2要素、第3要素も同様。
p142 \(\mathrm{div}(\rho v_x\vec{v})\) の縮約記法による表現
\begin{eqnarray}\mathrm{div}(\rho v_x\vec{v})&=&\mathrm{div}\left(\begin{array}{x}\rho v_xv_x\\\rho v_xv_y\\ \rho v_xv_z\end{array}\right)\nonumber\\&=&\frac{\partial(\rho v_xv_x)}{\partial x_1}+\frac{\partial(\rho v_xv_y)}{\partial x_2}+\frac{\partial(\rho v_xv_z)}{\partial x_3}\nonumber\\&=&\frac{\partial U_{11}}{\partial x_1}+\frac{\partial U_{12}}{\partial x_2}+\frac{\partial U_{13}}{\partial x_3}\nonumber\\&=&\frac{\partial U_{1j}}{\partial x_j}\nonumber\end{eqnarray}となる(走る添え字 \(j\) は、数値1, 2, 3 をとるものとする)。
これを領域\(V\) で体積分したものが、\[\int_V\frac{\partial U_{1j}}{\partial x_j}~dV\]であり、p142の式2.06の左辺の第1要素である(同式では\(j\) を \(i\)へと表記替え)。
p142 式2.06
\[\int_V\frac{\partial \vec{U}}{\partial \vec{x}}~dV\]は、『\(\vec{U}\) を\(\vec{x}\) で偏微分したものを体積分したもの』ではなく、左辺にあるとおり、3つの体積分を要素として持つベクトル。
p143 閉曲面\(S\) の表面に働く面積力
式2.08の1~2行目は、各要素にガウスの発散定理を用いて変形している。
p143 閉局面\(S\) 内の領域\(V\) の流体に働く体積力
単位質量当たりの力\[\vec{F}~~\left[\frac{N}{kg}\right]\]に密度\(\rho~~\left[\frac{kg}{m^3}\right]\) を乗じたものが、\[\rho \vec{F} ~~\left[\frac{N}{m^3}\right]\]これを領域\(V\) で体積分したものが、\[\int_V \rho \vec{F}~dV~~[N]\]
p144 単位時間あたり単位面積あたりの流入する運動量
単位時間・単位面積では、質量 \(\rho \vec{v}\cdot\vec{n}\) の流体が流れ出るところ、これに速度\(\vec{v}\) を乗じたものが運動量であるから、その運動量は、p142にあるとおり、\[(\rho\vec{v}\cdot\vec{n})\vec{v}\]である。
流入する運動量の場合、符号を逆転させ、\[-(\rho\vec{v}\cdot\vec{n})\vec{v}\]となる。
p145 2~4行目[第 \(i\) 成分の表示]
4行目左の式\[\frac{\partial U_{1j}}{\partial x_j}=\mathrm{div}(\rho v_1\vec{v})\]は、p142の式2.05である(走る添え字 \(j\) は数値\(1,2,3\)をとる)。これは、p142の\[\vec{U}=U_{ij}\]の1行目の横ベクトル \(U_{1j}\) を、\(x\) 座標(\(x_1,~x_2,~x_3\))で拡散\(\mathrm{div}\) したものである。
p145 7~9行目
7行目と同様の式は、\(v_x\) (\(x\) 座標表記の場合は\(=v_1)\) のみならず、\(v_y(=v_2),~v_z(=v_3)\) との関係でも成立するから、\[\left\{\begin{array}{x}\mathrm{div}(\rho v_x\vec{v})=\rho\vec{v}\cdot\mathrm{grad}v_x+v_x\mathrm{div}(\rho\vec{v})\\\mathrm{div}(\rho v_y\vec{v})=\rho\vec{v}\cdot\mathrm{grad}v_y+v_y\mathrm{div}(\rho\vec{v})\\\mathrm{div}(\rho v_z\vec{v})=\rho\vec{v}\cdot\mathrm{grad}v_z+v_z\mathrm{div}(\rho\vec{v})\end{array}\right.\]\(x\) 座標(\(x_1,~x_2,~x_3\))表記では、\[\left\{\begin{array}{x}\mathrm{div}(\rho v_{x_1}\vec{v})=\rho\vec{v}\cdot\mathrm{grad}v_{1}+v_{1}\mathrm{div}(\rho\vec{v})\\\mathrm{div}(\rho v_{x_2}\vec{v})=\rho\vec{v}\cdot\mathrm{grad}v_{2}+v_{2}\mathrm{div}(\rho\vec{v})\\\mathrm{div}(\rho v_{x_3}\vec{v})=\rho\vec{v}\cdot\mathrm{grad}v_{3}+v_{3}\mathrm{div}(\rho\vec{v})\end{array}\right.\]行列 \(U\) を用いて左辺を表現すると、\[\left\{\begin{array}{x}\frac{\partial U_{1j}}{\partial x_j}=\rho\vec{v}\cdot\mathrm{grad}v_{1}+v_{1}\mathrm{div}(\rho\vec{v})\\\frac{\partial U_{2j}}{\partial x_j}=\rho\vec{v}\cdot\mathrm{grad}v_{2}+v_{2}\mathrm{div}(\rho\vec{v})\\\frac{\partial U_{3j}}{\partial x_j}=\rho\vec{v}\cdot\mathrm{grad}v_{3}+v_{3}\mathrm{div}(\rho\vec{v})\end{array}\right.\]左辺は、止まっている添え字 \(i\) (数値1,2,3をとるものとする)を用いて表記を変換し、\begin{eqnarray}\left.\begin{array}{x}\frac{\partial U_{1j}}{\partial x_j}\\\frac{\partial U_{2j}}{\partial x_j}\\\frac{\partial U_{3j}}{\partial x_j}\end{array}\right\}&=&\frac{\partial U_{ij}}{\partial x_j} \nonumber\\&=&\frac{\partial \vec{U}}{\partial \vec{x}}\nonumber\end{eqnarray}のように、3行をまとめた行列(p142のベクトル \(\vec{U},~\vec{x}\))での表記ができる。
右辺の第1項も、p145赤字表記に従うとすれば、3行をまとめた以下のベクトル表記ができる。
\begin{eqnarray}\left.\begin{array}{x}\rho \vec{v}\cdot \mathrm{grad}v_1\\\rho \vec{v}\cdot \mathrm{grad}v_2\\\rho \vec{v}\cdot \mathrm{grad}v_3\end{array}\right\}&=&\rho\vec{v}\cdot \left(\begin{array}{x}\mathrm{grad}v_1\\\mathrm{grad}v_2\\\mathrm{grad}v_3\end{array}\right)\nonumber\\&=&\rho(\vec{v}\cdot \mathrm{grad})\vec{v}\nonumber\end{eqnarray}
*この表記法は、通常の表記法(\(\mathrm{grad}\cdots\) のような表記法)と異なり、勾配の対象「\(\cdots\)」が 、\(\mathrm{grad}\) の直後に位置していない。括弧の外右側に位置する \(\vec{v}\) について、順次、(1)その各要素に勾配の演算を実施した後、(2)左側の \(\vec{v}\) との内積の演算を行う趣旨である。
右辺の第2項も、3行をまとめた以下のベクトル表記ができる。\begin{eqnarray}\left.\begin{array}{x}v_1\mathrm{div}(\rho\vec{v})\\v_2\mathrm{div}(\rho\vec{v})\\v_3\mathrm{div}(\rho\vec{v})\end{array}\right\}&=&\mathrm{div}(\rho\vec{v})\left(\begin{array}{x}v_1\\v_2\\v_3\end{array}\right)\nonumber\\&=&\mathrm{div}(\rho\vec{v})\vec{v}\nonumber\end{eqnarray}
よって、ベクトルの式にまとめた結果は、p145の9行目のようになる。
p145 \(\frac{\partial (\rho\vec{v})}{\partial t}\) の時間 \(t\) による微分実行
\(\rho,~\vec{v}\) が、いずれも時間 \(t\) の関数である場合、ライプニッツ則(p26)\[(fg)'=f'g+fg'\]により、\[\frac{\partial (\rho\vec{v})}{\partial t}=\frac{\partial \rho}{\partial t}\vec{v}+\rho\frac{\partial \vec{v}}{\partial t}\]となる。
p147 \(p\delta_{ij}\)
\[\delta_{ij}=\left\{\begin{array}{x}1\cdots if~ (i=j)\\0\cdots if~(i\neq j)\end{array}\right.\]なので、\(i\) と \(j\) とが1, 2, 3 と変化するとき、
- \(\delta_{11}=\delta_{22}=\delta_{33}=1\)
- \(\delta_{12}=\delta_{13}=\delta_{21}=\delta_{23}=\delta_{31}=\delta_{32}=0\)
これを、\(i\) 行 \(j\) 列の行列で表現すると、\[\delta_{ij}=\left(\begin{array}{x}1&&0&&0\\0&&1&&0\\0&&0&&1\end{array}\right)\]よって、\[p\delta_{ij}=\left(\begin{array}{x}p&&0&&0\\0&&p&&0\\0&&0&&p\end{array}\right)\]
p147 \(\int_V \frac{\partial U_{ij}}{\partial x_j}~dV\)
末尾から7行目の[成分表示式]の右辺第1項 \[\int_V \frac{\partial U_{ij}}{\partial x_j}~dV\]は、p142の式2.05及び2.06と同じもの。
計算手順は、以下のとおり。
- \(\frac{\partial U_{11}}{\partial x_1}+\frac{\partial U_{12}}{\partial x_2}+\frac{\partial U_{13}}{\partial x_3}\) を計算して、\(\frac{\partial U_{1j}}{\partial x_j}\) を求める。
- \(\frac{\partial U_{1j}}{x_j}\) を体積分して、\(\int_V\frac{\partial U_{1j}}{x_j}~dV\)を求める。
- 同様にして、\(\int_V\frac{\partial U_{2j}}{x_j}~dV\) と \(\int_V\frac{\partial U_{3j}}{x_j}~dV\) も求める。
- \(\int_V\frac{\partial U_{1j}}{x_j}~dV\) と \(\int_V\frac{\partial U_{2j}}{x_j}~dV\) と \(\int_V\frac{\partial U_{3j}}{x_j}~dV\) の3つの要素を持つベクトルを組む。
末尾行の右辺にある\[\int_V\frac{\partial T_{ij}}{\partial x_j}~dV\]も同様。『\(T_{ij}\) を\(x_{j}\) で偏微分したものを体積分したもの』ではない。
p148 運動量の時間微分は力
- 時間を\(t\)
- 質量を\(m\)
- 速度を\(v\)
- 加速度を\(a\)
- 力を\(F\)
とすると、運動量\(mv\) の時間微分は、
\begin{eqnarray}\frac{d}{dt}(mv)&=&m\frac{d}{dt}v\nonumber\\&=&ma\nonumber\\&=&F\nonumber\end{eqnarray}
p150 電磁気の法則
\[F=\frac{1}{4\pi\varepsilon}\frac{qQ}{r^2}\]
\[F=qvB\]
\[H=\frac{I}{2\pi r}\]
\[V=-\frac{d\Phi}{dt}\]
p154 複数の電荷 \(A_1,~A_2,\cdots\)を含む閉曲面 \(S\) と点 \(B\)
点 \(B\) は、閉曲面 \(S\) 内、 閉曲面 \(S\) 上、閉曲面 \(S\) 外に存在し得る。
p156 微小面 \(T\)
点 \(B\) の位置 \(\vec{x}\) の微小面 \(T\) は、閉曲面 \(S\) 内・上・外に存在し得るが、式2.17\[\int_S \overrightarrow{E(\vec{x})}\cdot\overrightarrow{n(\vec{x})}~d\vec{x}=\frac{Q}{\varepsilon}\]は、複数の電荷 \(A_1,~A_2,\cdots\)を含む任意の閉曲面について成立するから、結局、そのような閉曲面であれば、閉曲面を貫通する全電気力線の本数 \(\int_S\overrightarrow{E(\vec{x})}\cdot\overrightarrow{n(\vec{x})}~d\vec{x}\) が、一定値 \(\frac{Q}{\varepsilon}\) となることを示している。
p157 2~12行目 数学的に厳密ではない導出
電荷 \(A_i\) の位置を \(x_i\)、 電荷 \(B\) の位置を \(x\) としていた表記法(p154)に従えば、
- 位置 \(\overrightarrow{x_i}\) での電荷密度が \(\rho(\overrightarrow{x_i})\)
- 式2.17は、\(\int_V\mathrm{div} \overrightarrow{E(\vec{x})}d\vec{x}=\frac{1}{\varepsilon}\int_V\rho(\overrightarrow{x_i})~d\overrightarrow{x_i}\)
- \(\mathrm{div}\overrightarrow{E\vec{x}}=\frac{\rho(\vec{x_i})}{\varepsilon}\) 極小領域(\(\vec{x}\fallingdotseq\overrightarrow{x_i}\))では、\(\mathrm{div}\overrightarrow{E\vec{x}}=\frac{\rho(\vec{x})}{\varepsilon}\)
- \(\mathrm{div}\overrightarrow{D\vec{x}}=\rho(\vec{x_i})\) 極小領域(\(\vec{x}\fallingdotseq\overrightarrow{x_i}\))では、\(\mathrm{div}\overrightarrow{D\vec{x}}=\rho(\vec{x})\)
となる。
p157 静電ポテンシャル \(\Phi(\vec{x})\)
位置 \(\vec{y}\) の電荷が生み出す位置 \(\vec{x}\) における電位 \(V\) のこと。
例えば、電荷 \(Q\)を中心とする半径 \(r\) の球体を考えると、
\begin{eqnarray}\Phi(\vec{x})&=&\frac{1}{4\pi\varepsilon}\int_V\frac{\rho(\vec{y})}{|\vec{y}-\vec{x}|}d\vec{y}\nonumber\\&=&\frac{1}{4\pi \varepsilon}\frac{Q}{r}\nonumber\end{eqnarray}
p157 末尾から4~3行目 \(\mathrm{grad}\frac{1}{|\vec{y}-\vec{x}|}\)
\begin{eqnarray}\mathrm{grad}\frac{1}{|\vec{y}-\vec{x}|}&=&\frac{\vec{y}-\vec{x}}{|\vec{y}-\vec{x}|^3}\nonumber\end{eqnarray}導出方法は、前掲「p127 \(\mathrm{grad}\frac{1}{|\vec{y}-\vec{x}|}\)」のとおり。
p158 \(\overrightarrow{E(\vec{x})}=-\mathrm{grad}\phi(\vec{x})\)
電荷群 \(A_i\) が、位置 \(\vec{x}\) にある点\(B\) に対して及ぼす電界 \(\overrightarrow{E(\vec{x})}\) は、 式2.16の \(n\) を無限大 \(\infty\) に近づけていくと( \(x_i\) を \(\vec{y}\) に置換え表示 )、\begin{eqnarray}\overrightarrow{E(\vec{x})}&=&\lim_{n\to \infty}\sum_{i=1}^n\frac{1}{4\pi\varepsilon}\frac{Q_i}{|\vec{x}-\vec{x_i}|^3}(\vec{x}-\vec{x_i})\nonumber\\&=&\int_V\frac{1}{4\pi\varepsilon}\frac{\rho(\vec{y})}{|\vec{x}-\vec{y}|^3}(\vec{x}-\vec{y})~d\vec{y}\nonumber\\&=&-\int_V\frac{1}{4\pi\varepsilon}\frac{\rho(\vec{y})}{|\vec{y}-\vec{x}|^3}(\vec{y}-\vec{x})~d\vec{y}\nonumber\\&=&-\frac{1}{4\pi\varepsilon}\int_V\rho(\vec{y})\left(\frac{\vec{y}-\vec{x}}{|\vec{y}-\vec{x}|^3}\right)~d\vec{y}\nonumber\\&=&-\mathrm{grad}\phi(\vec{x})\nonumber\end{eqnarray}すなわち、静電ポテンシャル \(\phi\) (=電位 \(V\))の勾配(各要素を微分。p60)が、電界(のマイナス)となる。
p158 \(\Delta\phi(\vec{x})=-\frac{\rho(\vec{x})}{\varepsilon}\)
静電ポテンシャル \(\phi\) (=電位 \(V\) )のラプラシアン \(\Delta\) (各要素を2階微分して合算。p61)は、\(\phi(\vec{x})\)の定義より(p157)、\begin{eqnarray}\Delta\phi(\vec{x})&=&\Delta\left(\frac{1}{4\pi\varepsilon}\int_V\frac{\rho(\vec{y})}{|\vec{y}-\vec{x}|}d\vec{y}\right)\nonumber\\&=&\frac{1}{\varepsilon}\Delta\left(\frac{1}{4\pi}\int_V\frac{\rho(\vec{y})}{|\vec{y}-\vec{x}|}d\vec{y}\right)\nonumber\end{eqnarray}これに定理1.39(p104)\begin{eqnarray}A(\vec{x})&=&\frac{1}{4\pi}\int_V\frac{f(\vec{y})}{|\vec{y}-\vec{x}|}d\vec{y}\nonumber\\ &\downharpoonleft&\nonumber\\\Delta A(\vec{x})&=&-f(\vec{x})\nonumber\end{eqnarray}を用いると、与式は、\begin{eqnarray}\Delta \phi(\vec{x})&=&\frac{1}{\varepsilon}\left(-\rho(\vec{x})\right)\nonumber\\&=&-\frac{\rho(\vec{x})}{\varepsilon}\nonumber\end{eqnarray}となる。
p162 物体を経路に沿って動かすときの仕事(線積分)
仕事 \(W\) は、力 \(F\) の接線方向の成分と微小距離の積(=力 \(F\)と接線ベクトルとの内積)を全経路にわたって合算したものであるから、曲線の接線ベクトルを \(\frac{d\vec{r}}{ds}\) とすると(パラメータ \(s\) による表示。p72)、
\begin{eqnarray}\lim_{n\to \infty}\sum_{i=1}^n\overrightarrow{F(X_i)}\cdot\Delta\vec{r_i}&=&\int_C\vec{F}\cdot\frac{d\vec{r}}{ds}~ds\nonumber\\&=&\int_C\vec{F}\cdot d\vec{r}\nonumber\end{eqnarray}として線積分により計算される。
p163 \(\int_C \mathrm{grad}\phi\cdot d\vec{r}\)
\begin{eqnarray}\int_C \mathrm{grad}\phi\cdot d\vec{r}&=&\int_C \mathrm{grad}\phi\cdot \frac{d\vec{r}}{ds}~ds\nonumber\\&=&\int_C \left(\begin{array}{x}\frac{\partial \phi}{\partial x}\\\frac{\partial \phi}{\partial y}\\\frac{\partial \phi}{\partial z}\end{array}\right)\cdot \left(\begin{array}{x}\frac{dx}{ds}\\\frac{dy}{ds}\\\frac{dz}{ds}\end{array}\right)~ds\nonumber\\&=&\int_C\left(\frac{\partial \phi}{\partial x}\frac{dx}{ds}+\frac{\partial \phi}{\partial y}\frac{dy}{ds}+\frac{\partial \phi}{\partial z}\frac{dz}{ds}\right)~ds\nonumber\end{eqnarray}ここで、3変数の連鎖律(p29 定理1.07)\[\frac{df}{dt}=\frac{\partial f}{\partial x}\frac{dx}{dt}+\frac{\partial f}{\partial y}\frac{dy}{dt}+\frac{\partial f}{\partial z}\frac{dz}{dt}\]を用いると、与式は、3変数微分から1変数微分へと圧縮表記でき、\begin{eqnarray}\int_C \mathrm{grad}\phi\cdot d\vec{r}&=&\int_C\frac{d\phi}{ds}ds\nonumber\\&=&\left[\phi\right]_{s=a}^{s=b}\nonumber\\&=&\left[\phi(\vec{x})\right]_{s=a}^{s=b}\nonumber\\&=&\left[\phi(\overrightarrow{r(s)})\right]_{s=a}^{s=b}\nonumber\\&=&\phi(\overrightarrow{r(b)})-\phi(\overrightarrow{r(a)})\nonumber\\&=&\phi(\vec{b})-\phi(\vec{a})\nonumber\end{eqnarray}となる。
p163 電場\(\vec{E}\) を線積分すると静電ポテンシャル(=電位)
\begin{eqnarray}\int_C-\vec{F}\cdot\vec{r}&=&q\left\{\phi(\vec{b})-\phi(\vec{a})\right\}\nonumber\\ \int_C-q\vec{E}\cdot d\vec{r}&=&q\left\{\phi(\vec{b})-\phi(\vec{a})\right\}\nonumber\\ \int_C-\vec{E}\cdot d\vec{r}&=&\phi(\vec{b})-\phi(\vec{a})\nonumber\end{eqnarray}
p164 \(-\mathrm{grad} V(x)\)
\(x\) 軸方向に電圧\(V\) がかけられているので、\(y,~z\) 軸方向への変化は存在しない。\[\left\{ \begin{array}{x}\frac{\partial V(x)}{\partial y}=0\\ \frac{\partial V(x)}{\partial z}=0\end{array} \right.\]
p165 電場\(\overrightarrow{E(r)}=-\mathrm{grad}\phi(r)\)
\(x\) 軸方向に\(\vec{r}\) の座標をとり、\[\vec{r}=\left(\begin{array}{x}r\\0\\0\end{array}\right)\]とすると、\begin{eqnarray}\overrightarrow{E(r)}&=&\frac{1}{4\pi \varepsilon}\frac{Q}{r^3}\vec{r}\nonumber\\&=&\frac{1}{4\pi \varepsilon}\frac{Q}{r^3}\left(\begin{array}{x}r\\0\\0\end{array}\right)\nonumber\\&=&\frac{1}{4\pi \varepsilon}\frac{Q}{r^2}\left(\begin{array}{x}1\\0\\0\end{array}\right)\nonumber\end{eqnarray}他方で、スカラー場\(\phi(r)\) のマイナス勾配は、\begin{eqnarray}-\mathrm{grad}\phi(r)&=&-\left(\begin{array}{x}\frac{\partial}{\partial x}\\ \frac{\partial}{\partial y}\\ \frac{\partial}{\partial z}\end{array}\right) \frac{1}{4\pi\varepsilon}\frac{Q}{r}\nonumber\\&=&-\frac{1}{4\pi\varepsilon}Q\left(\begin{array}{x}\frac{\partial}{\partial x}\\ \frac{\partial}{\partial y}\\ \frac{\partial}{\partial z}\end{array}\right) r^{-1}\nonumber\\&=&-\frac{1}{4\pi\varepsilon}Q\left(\begin{array}{x}\frac{\partial}{\partial x}r^{-1}\\ \frac{\partial}{\partial y}r^{-1}\\ \frac{\partial}{\partial z}r^{-1}\end{array}\right) \nonumber\end{eqnarray}ここで、\(r\) は、\(x\) 軸上の数値であるので、\begin{eqnarray}\frac{\partial}{\partial x}r^{-1}&=&-r^{-2}\nonumber\\&=&-\frac{1}{r^2}\nonumber\end{eqnarray}である。
また、\(r\) は、\(y,~z\)軸では変化しないから、\(\frac{\partial}{\partial y}r^{-1},~\frac{\partial}{\partial z}r^{-1}\) は、0 である。
よって、与式は、\begin{eqnarray}-\mathrm{grad}\phi(r)&=&-\frac{1}{4\pi\varepsilon}Q\left(\begin{array}{x}-\frac{1}{r^2}\\0\\0\end{array}\right)\nonumber\\&=&\frac{1}{4\pi \varepsilon}\frac{Q}{r^2}\left(\begin{array}{x}1\\0\\0\end{array}\right)\nonumber\end{eqnarray}従って、\[\overrightarrow{E(r)}=-\mathrm{grad}\phi(r)\]が成立する。
p165 \(\phi(a),~\phi(\infty)\)
\[\phi(r)=\frac{1}{4\pi\varepsilon}\frac{Q}{r}\]に各数値を代入すると、\[\phi(a)=\frac{1}{4\pi\varepsilon}\frac{Q}{a}\] であり、\begin{eqnarray} \phi(\infty)&=&\frac{1}{4\pi\varepsilon} \frac{Q}{\infty} \nonumber \\&=&0\nonumber \end{eqnarray} である。
p166 末尾5~4行目
公式1.18(p61)を用いて、\[(\mathrm{div}\vec{E})\phi=\mathrm{div}(\phi\vec{E})-\mathrm{grad}\phi\cdot\vec{E}\]と変形している。
p167 オーダー(桁)論
\(\phi(r)\) は、
\[\phi(r)=\frac{1}{4\pi\varepsilon}\frac{Q}{r}\]なので、\(\frac{1}{r}\) 関数。
他方で、\(E(r)\) は、\begin{eqnarray}E(r)&=&|\vec{E}|\nonumber\\&=&\left|\frac{1}{4\pi \varepsilon}\frac{Q}{r^2}\left(\begin{array}{x}1\\0\\0\end{array}\right)\right|\nonumber\\&=&\frac{1}{4\pi\varepsilon}\frac{Q}{r^2}\nonumber\end{eqnarray}なので、\(\frac{1}{r^2}\) 関数。
球面\(S\) の表面積は、\[S(r)=4\pi r^2\]であり、\(r^2\) 関数。
このため、第1項(\(\phi\vec{E}\) の面積分)は、\begin{eqnarray}\frac{1}{2}\varepsilon_0\int_S\phi\vec{E}\cdot\vec{n}dS&\propto&\frac{1}{r}\frac{1}{r^2}r^2\nonumber\\&=&\frac{1}{r}\nonumber\end{eqnarray}となり、\(r\rightarrow\infty\) のとき、0 となる。
p167 静電場のエネルギー密度
静電場のエネルギー\(U~[J]\) の単位体積あたりの量。
単位は、\[\left[\frac{J}{m^3}\right]\]
p169 \(H\) を\(C\) について線積分
半径\(r\) の円である曲線\(C\) の磁場ベクトル\(\overrightarrow{H(\vec{x})}\) は、曲線\(C\) の単位接線ベクトル\(\overrightarrow{n(\vec{x}})\)と同じ方向であるから(ベクトル内角\(\theta=0\))、両ベクトルの内積は、\begin{eqnarray}\vec{H}\cdot\vec{n}&=&|\vec{H}||\vec{n}|\cos\theta\nonumber\\&=&|\vec{H}|\times 1\times 1\nonumber\\&=&H\nonumber\end{eqnarray}これを円周\(2\pi r\) 倍したものが線積分であるから、\begin{eqnarray}\int_C\vec{H}\cdot \vec{n}d\vec{x}&=&H\times 2\pi r\nonumber\end{eqnarray}
p170 電流密度 \( \overrightarrow{i(\vec{x})} \)
電流密度 \( \overrightarrow{i(\vec{x})} \)は、位置\(x\) における面積あたり時間あたり通過電気量。
単位は、\[\left[\frac{Q}{m^2\cdot s}\right]\]これに通過面積\(S\)を乗じたものが、電流\(I\) であり、
その単位は、毎秒あたり通過電気量として、\[\left[\frac{Q}{s}\right]=[A]\]とあらわされる。
p170 \(\mathrm{div}~\overrightarrow{i(\vec{x})}=0\)
電流の値が一定(時間変化がない)の場合、微小直方体に流入する電荷と流出する電荷の両が等しい(p43)。
p170 電荷の保存則
磁界\(\vec{H}\) の回転は、電場\(\vec{D}\)の時間変化及び電流密度\(\vec{i}\) の和に等しい。\[\mathrm{rot}\vec{H}=\frac{\partial}{\partial t}\vec{D}+\vec{i}\]
p171 磁束密度\(B\)、透磁率\(\mu\)、磁束\(\Phi\)
\begin{eqnarray}\left\{\begin{array}{x}\vec{B}&=&\mu\vec{H}\\ \Phi&=&|\vec{B}|\times S\nonumber\\ V&=&-\frac{d}{dt}\Phi\end{array}\right.\end{eqnarray}
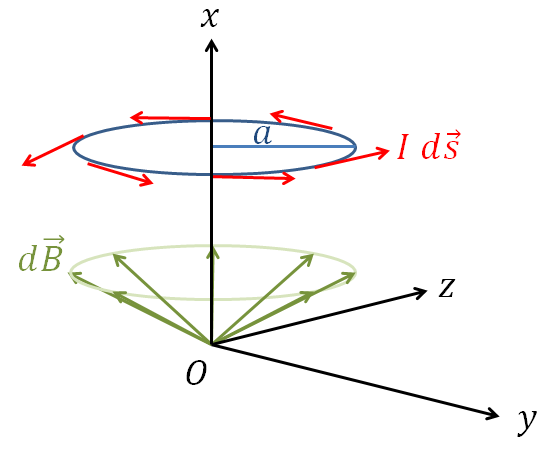
p172 \(I~d\vec{s}\)
アンペールの法則より、\[|\vec{B}|\propto I\]その微小部分については、\(d|\vec{B}|\propto dI\) となりそうだが、電流\(I\) は電線のどの箇所でも一定値であることを踏まえると、微小な電線部分を\(d\vec{s}\) として、\[d|\vec{B}|\propto I~d\vec{s}\]と置ける。
p173 \(\frac{\vec{x}-\vec{y}}{|\vec{x}-\vec{y}|}\)
\[\frac{\vec{x}-\vec{y}}{|\vec{x}-\vec{y}|}\]は、分母と分子の大きさが同じであり分数全体の大きさは\(1\) 。
ベクトルの方向は、分子により、位置\(y\)から位置\(x\)へ向いている。
この結果、分数全体で、p172右図の点線方向(\(y\)から\(x\)への方向)の単位方向ベクトルを示している。
\(d\vec{s}\) とこの単位方向ベクトルとの外積として得られるベクトルの方向(=\(d\vec{B}\)の方向)は、p21 の定義に従い、紙面前から紙面奥への方向となる。
p174 \(x=r\tan\theta\) の\(\theta\)微分
\(\theta\) による微分を\('\) 表記することにすると、p26のライプニッツ則・連鎖律を用いて、\begin{eqnarray}\tan'\theta&=&\left(\frac{\sin\theta}{\cos\theta}\right)'\nonumber\\&=&\sin\theta\left(\frac{1}{\cos\theta}\right)'+\sin'\theta\frac{1}{\cos\theta}\nonumber\\&=&\sin\theta\left(\cos'\theta\times\frac{d}{d(\cos\theta)}\cos^{-1}\theta\right)+\cos\theta\frac{1}{\cos\theta}\nonumber\\&=&\sin\theta\left\{-\sin\theta\times (-\cos^{-2}\theta)\right\}+1\nonumber\\&=&\sin^2\theta\frac{1}{\cos^2\theta}+1\nonumber\\&=&\frac{\sin^2\theta+\cos^2\theta}{\cos^2\theta}\nonumber\\&=&\frac{1}{\cos^2\theta}\nonumber\end{eqnarray}となるので、
\(x=r\tan\theta\) の両辺を\(\theta\) で微分すると、\begin{eqnarray}\frac{d}{d\theta}x&=&\frac{d}{d\theta}r\tan\theta\nonumber\\&=&r \frac{d}{d\theta}\tan\theta\nonumber\\&=&\frac{r}{\cos^2\theta}\nonumber\end{eqnarray}となる。
左辺は、\(\theta\) を微小変化させたときの\(x\) の微小変化であるから、微小変化(微分)を分母と分子に持つ分数\(\frac{dx}{d\theta}\) と見て良いので、上記式の両辺に、微分\(d\theta\) を乗ずることができ、\[dx=\frac{r}{\cos^2\theta}d\theta\]が得られる。
p174 \(d\vec{x}\times \overrightarrow{PA}\) の大きさ
外積の大きさは、両ベクトルが張る平行四辺形の面積に等しい(p21)。
同平行四辺形の面積は、p173 の図で底辺の長さが\(dx\) 、高さ\(r\) のものであるから、\begin{eqnarray}\left|d\vec{x}\times \overrightarrow{PA}\right|&=&r~dx\nonumber\\&=&r\frac{r}{\cos^2\theta}d\theta\nonumber\end{eqnarray}
p174 \(\int_{-\infty}^{\infty}\cdots dx\) の置換積分
\(x\) を\(-\infty\) から\(\infty\) まで変化させるとき、\(\theta\) は、\(-\frac{\pi}{2}\) から\(\frac{\pi}{2}\) まで変化するので、\begin{eqnarray}B&=&\int_{-\infty}^{\infty}\cdots dx\nonumber\\&=&\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}}\cdots d\theta\nonumber\end{eqnarray}と置換して積分することができる。
p175 \(d\vec{B}\) の向き
図の\(d\vec{B}\) の方向図示は逆向きか。
p175 \(|d\vec{s}\times \overrightarrow{PO}|\)
外積の大きさは、両ベクトルの絶対値と正弦 \(\sin\theta\)を乗じたものであるから(p22)、\(d\vec{s}\) と\(\overrightarrow{PO}\) が直交していることを踏まえると、\begin{eqnarray}\left|d\vec{s}\times \overrightarrow{PO}\right|&=&|d\vec{s}|\left|\overrightarrow{PO}\right|\sin\frac{\pi}{2}\nonumber\\&=&|d\vec{s}|PO\times 1\nonumber\\&=&|d\vec{s}|PO\nonumber\end{eqnarray}
p175 コイル1周分の積分で \(x\) 軸方向以外は打ち消しあう
コイルの周上を点\(P\) が一周する場合、微小電流 \(I ~d\vec{s}\) と \(\overrightarrow{PO}\) の外積を方向ベクトルとして含む磁束密度 \(d \vec{B}\) は、(\(y,~z\)) 平面では、原点\(O\) を中心とする円運動を描く。よって、コイル1周分で積算すると、\(y,~z\) 軸方向の成分はプラス・マイナスで打ち消しあい、0 となる。
このため、\(d\vec{B}\) の \(x\) 軸方向のみの要素(\(d\vec{B}\) が \(x\) 軸に対して \(\theta\) の角度を保つことから、\(\cos\theta\) を乗じたもの)の1周分の積算をすればよい。
p176 1~2行目 置換積分
\(x\)から\(\theta\) への置換積分。
\(x\) を\(-\infty\) から\(\infty\) まで変化させるとき、\(\theta\) は、\(-\frac{\pi}{2}\) から\(\frac{\pi}{2}\) まで変化する。
p176 \(\mathrm{rot}\left(\frac{\overrightarrow{i(\vec{y})}}{|\vec{x}-\vec{y}|}\right)\)
\begin{eqnarray}\mathrm{rot}\left(\frac{\overrightarrow{i(\vec{y})}}{|\vec{x}-\vec{y}|}\right)&=&\bigtriangledown\left(\frac{\overrightarrow{i(\vec{y})}}{|\vec{x}-\vec{y}|}\right)\nonumber\\&=&\left(\begin{array}{x}\frac{\partial}{\partial x_1}\\ \frac{\partial}{\partial x_2} \\ \frac{\partial}{\partial x_3} \end{array}\right)\times\left(\frac{\overrightarrow{i(\vec{y})}}{|\vec{x}-\vec{y}|}\right)\nonumber\\&=&\left(\begin{array}{x}\frac{\partial}{\partial x_1}\\ \frac{\partial}{\partial x_2} \\ \frac{\partial}{\partial x_3} \end{array}\right)\times\left(\begin{array}{x}\frac{\overrightarrow{i_1(\vec{y})}}{|\vec{x}-\vec{y}|}\\\frac{\overrightarrow{i_2(\vec{y})}}{|\vec{x}-\vec{y}|}\\\frac{\overrightarrow{i_3(\vec{y})}}{|\vec{x}-\vec{y}|}\end{array}\right)\nonumber\\&=&\left(\begin{array}{c}\frac{\partial}{\partial x_2}\left(\frac{\overrightarrow{i_3(\vec{y})}}{|\vec{x}-\vec{y}|}\right) -\frac{\partial}{\partial x_3}\left(\frac{\overrightarrow{i_2(\vec{y})}}{|\vec{x}-\vec{y}|}\right)\\ \cdots\\ \cdots\end{array}\right)\nonumber\end{eqnarray}この行列の第1行目を検討する。\(\vec{y}\) は、\(\left(\begin{array}{x}y_1\\y_2\\y_3\end{array}\right)\) であり、\(x_2,~x_3\) との関係では、定数であるから、行列の第1行目は、p177 の2~3行目のように、変形できる。
p177 \(\frac{\partial}{\partial x_2}\left(\frac{1}{|\vec{x}-\vec{y}|}\right)\)
3行目第1項の \(i_3(\vec{y})\frac{\partial}{\partial x_2}\left(\frac{1}{|\vec{x}-\vec{y}|}\right)\) に含まれる偏微分の箇所は、
第1章 数学の準備 [p110 赤字部分(公式1.35の gradf を計算するときの要領]と同様に、\(|\vec{x}-\vec{y}|^2=u\) と置くことで、以下のように変形できる。\begin{eqnarray}\frac{\partial}{\partial x_2}\left(\frac{1}{|\vec{x}-\vec{y}|}\right)&=&\frac{\partial}{\partial x_2}u\times \frac{\partial}{\partial u}\frac{1}{\sqrt{u}}\nonumber\end{eqnarray}この計算を実行すると、\begin{eqnarray}\frac{\partial}{\partial x_2}\frac{1}{|\vec{x}-\vec{y}|}&=&\frac{\partial}{\partial x_2}u\times \frac{\partial}{\partial u}\frac{1}{\sqrt{u}}\nonumber\\&=&\frac{\partial}{\partial x_2}\left\{(x_1-y_1)^2+(x_2-y_2)^2+(x_3-y_3)^2\right\}\times \frac{\partial}{\partial u}u^{\frac{-1}{2}}\nonumber\\&=&\frac{\partial}{\partial x_2}(\cdots x_2^2-2x_2y_2+y_2^2+\cdots)\times \left(-\frac{1}{2}\right)u^{\frac{-3}{2}}\nonumber\\&=&(2x_2-2y_2)\times \left(\frac{-1}{2}\right)\frac{1}{u^{\frac{3}{2}}}\nonumber\\&=&-(x_2-y_2)\frac{1}{|\vec{x}-\vec{y}|^{2\times\frac{3}{2}}}\nonumber\\&=&-(x_2-y_2)\frac{1}{|\vec{x}-\vec{y}|^3}\nonumber\\&=&-\frac{x_2-y_2}{|\vec{x}-\vec{y}|^3}\nonumber\end{eqnarray}となる(*)。
なお、表記上、p177 の赤字注のように、\(x_2-y_2\) のことを \((\vec{x}-\vec{y})_2\) の如く、ベクトル下添字によりベクトルの特定成分を表現することとした場合には、最後の部分は、\[=-\frac{(\vec{x}-\vec{y})_2}{|\vec{x}-\vec{y}|^3}\]となる。
*\(|\vec{x}-\vec{y}|=\left|\left(\begin{array}{c}x_1-y_1\\x_2-y_2\\x_3-y_3\end{array}\right)\right|=\sqrt{(x_1-y_1)^2+(x_2-y_2)^2+(x_3-y_3)^2}=\sqrt{u}\) を用いた。
p177 \(\frac{\overrightarrow{i(\vec{y})}\times(\vec{x}-\vec{y})}{|\vec{x}-\vec{y}|^3}\) の第1成分
\begin{eqnarray}\frac{\overrightarrow{i(\vec{y})}\times(\vec{x}-\vec{y})}{|\vec{x}-\vec{y}|^3}&=&\frac{1}{|\vec{x}-\vec{y}|^3}\left(\begin{array}{c}i_1(\vec{y})\\i_2(\vec{y})\\i_3(\vec{y})\end{array}\right)\times \left(\begin{array}{c}x_1-y_1\\ x_2-y_2\\ x_3-y_3\end{array}\right)\nonumber\\&=&\frac{1}{|\vec{x}-\vec{y}|^3}\left(\begin{array}{c}i_2(\vec{y})(x_3-y_3)-i_3(\vec{y})(x_2-y_2)\\ \cdots \\ \cdots\end{array}\right)\nonumber\end{eqnarray}となるので、第1成分は、\begin{eqnarray}\frac{1}{|\vec{x}-\vec{y}|^3}\left\{i_2(\vec{y})(x_3-y_3)-i_3(\vec{y})(x_2-y_2)\right\}&=&i_2(\vec{y})\frac{x_3-y_3}{|\vec{x}-\vec{y}|^3}-i_3(\vec{y})\frac{x_2-y_2}{|\vec{x}-\vec{y}|^3}\nonumber\end{eqnarray}となり、p177 の4行目と一致する。
第2成分、第3成分についても、同様に一致する。
よって、問題2.14の等式が成立する。
p181 平行四辺形(\(\vec{v}\Delta t\times d\vec{r}\))を貫く磁束の本数 \(\Delta \eta\)
位置 \(\vec{x}\) における磁束密度を \(\overrightarrow{B(\vec{x})}\) とし、位置 \(\vec{x}\) で微小面\(T\)(面積は\(\Delta S\)。単位法線ベクトルが \(\overrightarrow{n(\vec{x})}\) となるような方向の面)を考えると、p156 の分析と同様に、\(T\) を貫く磁束の本数は、\[\overrightarrow{B(\vec{x})}\cdot \overrightarrow{n(\vec{x})}\Delta S\]ここで、\(\vec{v}\Delta t\times d\vec{r}\) は、外積の定義から(p21)、その絶対値は両ベクトルで貼られる平行四辺形の面積に等しく、かつ、同外積の向きは同平行四辺形の法線方向であるから、\[\vec{v}\Delta t\times d\vec{r}=\overrightarrow{n(\vec{x})}\Delta S\]である。
よって、同外積をもって単位法線ベクトル \(\overrightarrow{n(\vec{x})}\) と微小面積 \(\Delta S\) とを置き換えることができる。
すなわち、平行四辺形(\(\vec{v}\Delta t\times d\vec{r}\))を貫く磁束の本数 \(\Delta \eta\) は、以下のようになる。\[\Delta \eta=\overrightarrow{B(\vec{x})}\cdot\vec{v}\Delta t\times d\vec{r} \]
p181 末尾8~7行目
\[\int_c\Delta \eta\]は、微小平行四辺形を貫く磁束の本数 \(\Delta\eta\) を、コイル\(C\) 全体を周回して線積分することで、斜柱側面全体面を貫く磁束の本数(=コイル\(C,~C'\) 間移動におけるコイルを貫く磁束の本数の変化)を計算している。
\[\frac{d\Phi}{dt}\]は、末尾8行目式を \(t\) で微分することで、誘導起電力を求めている。
同微分により、\(\Delta t\) が消去される。
\[\overrightarrow{B(\vec{x})}\times \vec{v}=-\vec{v}\times\overrightarrow{B(\vec{x})}\]は、ベクトル積の交換法則(p20)による。
p184 2~5行目 \(\frac{\partial}{\partial t}\mathrm{rot}\overrightarrow{B(\vec{x},t)}\)
式2.29(p183)より、\[\mathrm{rot}\overrightarrow{B(\vec{x},t)}=\varepsilon_0\mu_0\frac{\partial\overrightarrow{E(\vec{x},t)}}{\partial t}\]両辺を \(t\) で偏微分すると、\[\frac{\partial}{\partial t}\mathrm{rot}\overrightarrow{B(\vec{x},t)}=\varepsilon_0\mu_0\frac{\partial^2\overrightarrow{E(\vec{x},t)}}{\partial t^2}\]よって、2行目第2項は、5行目第2項のとおり置き換えできる。
p184 9~12行目 \(\frac{\partial}{\partial t}\mathrm{rot}\overrightarrow{E(\vec{x},t)}\)
式2.27(p183)より、\[\mathrm{rot}\overrightarrow{E(\vec{x},t)}=-\frac{\partial\overrightarrow{B(\vec{x},t)}}{\partial t}\]両辺を \(t\) で偏微分すると、\[\frac{\partial}{\partial t}\mathrm{rot}\overrightarrow{E(\vec{x},t)}=-\frac{\partial^2\overrightarrow{B(\vec{x},t)}}{\partial t^2}\]よって、9行目第2項は、12行目第2項のとおり置き換えできる。
p185 \(\frac{\partial}{\partial x}\left\{Ce_x\sin(\vec{k}\cdot\vec{x}-ct+\alpha)\right\}\)
合成関数の微分の公式(p26)により、
\begin{eqnarray}\frac{\partial}{\partial x}\left\{Ce_x\sin(\vec{k}\cdot\vec{x}-ct+\alpha)\right\}&=&Ce_x\frac{\partial}{\partial x}\sin(\vec{k}\cdot\vec{x}-ct+\alpha)\nonumber\\&=&Ce_x\frac{\partial}{\partial x}(\vec{k}\cdot\vec{x}-ct+\alpha)\times\frac{\partial}{\partial(\vec{k}\cdot\vec{x}-ct+\alpha)}\sin(\vec{k}\cdot\vec{x}-ct+\alpha)\nonumber\end{eqnarray}と変形できる。
ここで、後半の微分は、三角関数の微分であるから(\(\vec{k}\cdot\vec{x}\) は内積でありスカラー値)、\[\frac{\partial}{\partial(\vec{k}\cdot\vec{x}-ct+\alpha)}\sin(\vec{k}\cdot\vec{x}-ct+\alpha)=\cos(\vec{k}\cdot\vec{x}-ct+\alpha)\]である。
前半の \(x\) による微分は、\(x\) 座標軸との関係では、\(x_1\) のみが変数であり、\(ct,~\alpha,~k_1,~k_2,~k_3,~x_2,~x_3\) は、いずれも定数であるから(\(x_2\) は\(y\) 軸、\(x_2\) は\(z\) 軸方向の変数である)、
\begin{eqnarray}\frac{\partial}{\partial x}(\vec{k}\cdot\vec{x})&=&\frac{\partial}{\partial x}\left(\begin{array}{c}k_x\\k_y\\k_z\end{array}\right)\cdot \left(\begin{array}{c}x_1\\x_2\\x_3\end{array}\right)\nonumber\\&=&\frac{\partial}{\partial x}(k_xx_1+k_yx_2+k_zx_3)\nonumber\\&=&\frac{\partial}{\partial x}(k_xx_1)\nonumber\\&=&k_x\nonumber\end{eqnarray}となる。
よって、与式は、以下のようになる。\[\frac{\partial}{\partial x}\left\{Ce_x\sin(\vec{k}\cdot\vec{x}-ct+\alpha)\right\}=Ce_xk_x\cos(\vec{k}\cdot\vec{x}-ct+\alpha)\]同様に計算することで、以下の2式も得られる。
\[\frac{\partial}{\partial y}\left\{Ce_y\sin(\vec{k}\cdot\vec{x}-ct+\alpha)\right\}=Ce_yk_y\cos(\vec{k}\cdot\vec{x}-ct+\alpha)\]
\[\frac{\partial}{\partial z}\left\{Ce_z\sin(\vec{k}\cdot\vec{x}-ct+\alpha)\right\}=Ce_zk_z\cos(\vec{k}\cdot\vec{x}-ct+\alpha)\]
これら3式を合計すると、p185の8行目の式が得られる。
p185 \(B(\vec{x},t)\) の\(x\) 成分 \(B_x(\vec{x},t)\)
\(B_x(\vec{x},t)\) を時間 \(t\) について偏微分すると、\begin{eqnarray}\frac{\partial}{\partial t}B_x(\vec{x},t)&=&\frac{\partial}{\partial t}\frac{1}{c}(k_ye_z-k_ze_y)C\sin(\vec{k}\cdot\vec{x}-ct+\alpha)\nonumber\\&=&\frac{1}{c}(k_ye_z-k_ze_y)C\frac{\partial}{\partial t}\sin(\vec{k}\cdot\vec{x}-ct+\alpha)\nonumber\end{eqnarray}ここで、\(\sin\) の中の \(\vec{k}\cdot\vec{x}\) はスカラー値であり\(t\) との関係では定数であり、\(\alpha\) も \(t\) との関係では定数であるから、偏微分の箇所は、合成関数の微分の公式(p26)により、\begin{eqnarray}\frac{\partial}{\partial t}\sin(\vec{k}\cdot\vec{x}-ct+\alpha)&=&\frac{\partial}{\partial t}(\vec{k}\cdot\vec{x}-ct+\alpha)\times \frac{\partial}{\partial (\vec{k}\cdot\vec{x}-ct+\alpha)}\sin(\vec{k}\cdot\vec{x}-ct+\alpha)\nonumber\\&=&\frac{\partial}{\partial t}(-ct)\times\cos(\vec{k}\cdot\vec{x}-ct+\alpha)\nonumber\\&=&-c~\cos(\vec{k}\cdot\vec{x}-ct+\alpha)\nonumber\end{eqnarray}である。
よって、与式は、\begin{eqnarray}\frac{\partial}{\partial t}B_x(\vec{x},t)&=&\frac{1}{c}(k_ye_z-k_ze_y)C\times -\left\{c~\cos(\vec{k}\cdot\vec{x}-ct+\alpha)\right\}\nonumber\\&=&-(k_ye_z-k_ze_y)C\cos(\vec{k}\cdot\vec{x}-ct+\alpha)\nonumber\end{eqnarray}となる。
すなわち、 末尾3行目の \(B_x(\vec{x},t)\) は、末尾5行目の式を充たす。
p186 \(E(\vec{x},t)\)
\(E(\vec{x},t)\) (p185の2行目の式)は、p103 の解釈から、\(k\) 方向に速度\(c\) で進む波であり、振幅の大きさは \(C|\vec{e}|\)、振幅の方向は\(\vec{e}\) 、位相の遅れは\(\alpha\) である。
また、185 で求めたとおり、\begin{eqnarray}\vec{k}\cdot\vec{e}&=&|\vec{k}||\vec{e}|\cos\theta\nonumber\\&=&0\nonumber\end{eqnarray} であるので、\(\cos\theta=0\) である。
すなわち、両ベクトルのなす角度 \(\theta\) は直角 (\(\theta=\frac{\pi}{2}\)) である。
p186 \((\vec{k}\times \vec{e})\) と \(\vec{e}\) とは直交
外積の性質(p21)より、\(\vec{k}\) から \(\vec{e}\) の方向へ回転させた場合の右ねじの進む向きが \(\vec{k}\times \vec{e}\) (紙面手前向きの赤色ベクトル)の向きとなる。
p188 \(\mathrm{rot}\vec{E}=0\)
電場\(\vec{E}\) は、式2.18(p158)より、\[\overrightarrow{E(\vec{x})}=-\mathrm{grad}\phi\]
p189 仕事率 \(w(t)\)
仕事率 \(w(t)\) は、単位時間内に仕事に使われるエネルギー。
仕事に使われるエネルギーを\(W\)、時間を\(t\) とすると、\[w(t)=\frac{dW}{dt}\]
単位は、\[\left[\frac{J}{s}\right]=[W]\]他方で、電力\(P\)は、単位時間に電流\(I\)がする仕事量であり、電圧を\(V\)とすると、\[P=VI\]よって、仕事率\(w(t)\) と電力\(P\)は、同等の概念。
末尾4行目の \(V\) は、プラス方向の座標を前提に計算している。
p189 \(\frac{\partial B(t)}{\partial t}B(t)\) の積分は、\(\frac{1}{2}B^2(t)\)
\(\frac{1}{2}B^2(t)\) の \(t\) による微分は、連鎖律(p26)より、\begin{eqnarray}\frac{\partial}{\partial t}\left(\frac{1}{2}B^2(t)\right)&=&\frac{1}{2}\frac{\partial}{\partial t }B^2(t)\nonumber\\&=&\frac{1}{2}\frac{\partial}{\partial t}B(t)\times\frac{\partial}{\partial B(t)}B(t)^2\nonumber\\&=&\frac{1}{2}\frac{\partial}{\partial t}B(t)\times2B(t)\nonumber\\&=&\frac{\partial}{\partial t}B(t)\times B(t)\nonumber\\&=&\frac{\partial B(t)}{\partial t}B(t)\nonumber\end{eqnarray}よって、\(\frac{\partial B(t)}{\partial t}B(t)\) の積分は、\(\frac{1}{2}B^2(t)\)
p190 5行目 静電場のエネルギー
静電場のエネルギーは、p167 にあるとおり、\[\frac{1}{2}\varepsilon_0E^2\]
p190 ジュール熱
ジュール熱の量を\(Q~[J]\) 、電圧を\(V\)、電流を\(I\)、通電時間を\(t\) とすると、ジュールの法則\[Q=VIt\]が成立している。
単位時間当たりに発生するジュール熱\(W~\left[\frac{J}{s}\right]\) は、\begin{eqnarray}W&=&\frac{Q}{t}\nonumber\\&=&VI\nonumber\end{eqnarray}である。なお、同単位は、\[\left[\frac{J}{s}\right]=[W(ワット)]\]とも表記される。
単位体積、単位時間あたりのジュール熱を \(w~\left[\frac{J}{s\cdot m^3}\right]\) とすると、抵抗の体積は、長さを\(l\)、断面積を\(\Delta S\) とすると、\(l\Delta S~[m^3]\) であるから、\[W=wl\Delta S~\left[\frac{J}{s}\right]\]である。
p191 ジュール熱の場の方程式
電場 \(\vec{E}\) と電流 \(\vec{i}\) のなす角度を \(\theta\) とすると、p161 のとおり、電流 \(\vec{i}\) 方向への電場 \(\vec{E}\) の大きさは、\[|\vec{E}|\cos\theta\]となる。
単位体積あたりの仕事率(単位体積・単位時間あたりのジュール熱)\(w\)は、p190 のとおり、両者の積\[|\vec{i}||\vec{E}|\cos\theta\]となる。
これは、内角の定義に従い、\[\vec{E}\cdot\vec{i}\]と表現できる。
よって、\[w=\vec{E}\cdot\vec{i}\]として、ジュール熱の場の方程式が導出される。
\(w\) の単位は、\[\left[\frac{J}{m^3\cdot s}\right]\]である。
p193 \(T^e\vec{n}=\left(\vec{T_x}\cdot\vec{n},~\vec{T_y}\cdot\vec{n},~\vec{T_z}\cdot\vec{n}\right)\)
行列の積として計算をすると、
\begin{eqnarray}T^e\vec{n}&=&\left(\begin{array}{c}T_{xx}&&T_{xy}&&T_{xz}\\T_{yx}&&T_{yy}&&T_{yz}\\T_{zx}&&T_{zy}&&T_{zz}\end{array}\right)\left(\begin{array}{c}n_x\\n_y\\n_z\end{array}\right)\nonumber\\&=&\left(\begin{array}{c}T_{xx}n_x+T_{xy}n_y+T_{xz}n_z\\T_{yx}n_x+T_{yy}n_y+T_{yz}n_z\\T_{zx}n_x+T_{zy}n_y+T_{zz}n_z\end{array}\right)\nonumber\end{eqnarray}他方で、\[T=\left(\begin{array}{c}\vec{T_x}\\ \vec{T_y}\\ \vec{T_z}\end{array}\right)\]とおくと、例えば、\[\vec{T_x}=\left(T_{xx}~T_{xy}~T_{xz}\right)\]と \(\vec{n}\) との内積は、\begin{eqnarray}\vec{T_x}\cdot \vec{n}&=&\left(T_{xx}~T_{xy}~T_{xz}\right)\left(\begin{array}{c}n_x\\n_y\\n_z\end{array}\right)\nonumber\\&=&T_{xx}n_x+T_{xy}n_y+T_{xz}n_z\nonumber\end{eqnarray}となり、行列の積の計算結果の1行目と同じである。
2行目、3行目についても、同様に一致が確認できる。
したがって、\[T^e\vec{n}=\left(\begin{array}{c}\vec{T_x}\cdot\vec{n}\\ \vec{T_y}\cdot\vec{n}\\ \vec{T_z}\cdot\vec{n}\end{array}\right)\]と整理できる。
p193 \(\frac{\partial T_{xx}}{\partial x}\)
\begin{eqnarray}\frac{\partial T_{xx}}{\partial x}&=&\frac{\partial}{\partial x}\left\{\varepsilon\left(E_x^2-\frac{1}{2}E^2\right)\right\}\nonumber\\&=&\frac{\varepsilon}{2}\frac{\partial}{\partial x}\left(2E_x^2-E^2\right)\nonumber\end{eqnarray}ここで、\(E=|\vec{E}|\) であることを踏まえると(p192)、
被微分関数 \(2E_x^2-E^2\) は、\begin{eqnarray}2E_x^2-E^2&=&2E_x^2-|\vec{E}|^2\nonumber\\&=&2E_x^2-(E_x^2+E_y^2+E_z^2)\nonumber\\&=&E_x^2-E_y^2-E_z^2\nonumber\end{eqnarray}なので、与式は、以下のようになる。\[\frac{\partial T_{xx}}{\partial x}=\frac{\varepsilon}{2}\frac{\partial}{\partial x}(E_x^2-E_y^2-E_z^2)\]
このうち第1項 \(\frac{\partial}{\partial x}E_x^2\) については、ライプニッツ則(p26)\[(fg)'=f'g+fg'\]を用いて、\begin{eqnarray}\frac{\partial}{\partial x}E_x^2&=&\frac{\partial E_x}{\partial x}E_x+E_x\frac{\partial E_x}{\partial x}\nonumber\\&=&2E_x\frac{\partial E_x}{\partial x}\nonumber\end{eqnarray}となる。
第2項 \(\frac{\partial}{\partial x}E_y^2\) についても、同様に、\begin{eqnarray}\frac{\partial}{\partial x}E_y^2&=&2E_y\frac{\partial E_y}{\partial x}\nonumber\end{eqnarray}となり、第3項 \(\frac{\partial}{\partial x}E_z^2\) についても、同様に、\begin{eqnarray}\frac{\partial}{\partial x}E_z^2&=&2E_z\frac{\partial E_z}{\partial x}\nonumber\end{eqnarray}となる。
よって、与式は、以下のように整理される。
\begin{eqnarray}\frac{\partial T_{xx}}{\partial x}&=&\frac{\varepsilon}{2}\left(2E_x\frac{\partial E_x}{\partial x}-2E_y\frac{\partial E_y}{\partial x}-2E_z\frac{\partial E_z}{\partial x}\right)\nonumber\\&=&\varepsilon\left(E_x\frac{\partial E_x}{\partial x}-E_y\frac{\partial E_y}{\partial x}-E_z\frac{\partial E_z}{\partial x}\right)\nonumber\end{eqnarray}
p193 \(\frac{\partial E_x}{\partial y}=\frac{\partial E_y}{\partial x}\)
電位ポテンシャル \(\phi\) の勾配は、マイナス電界 \(\vec{E}\) なので(p165)、\begin{eqnarray}\vec{E}&=&-\mathrm{grad}\phi\nonumber\\ \left(\begin{array}{c}E_x\\E_y\\E_z\end{array}\right)&=&\left(\begin{array}{c}-\frac{\partial\phi}{\partial x}\\-\frac{\partial\phi}{\partial y}\\-\frac{\partial\phi}{\partial z}\end{array}\right)\nonumber\\ \left(\begin{array}{c}E_x~\partial x\\E_y~\partial y\\E_z~\partial z\end{array}\right)&=&\left(\begin{array}{c}-\partial\phi\\-\partial\phi\\-\partial\phi\end{array}\right)\nonumber\end{eqnarray}となる(右辺の分数は微小部分の分数とみなせるので、各分母\(\partial x,~\partial y,~\partial z\)を両辺に乗じた)。
1行目と2行目とを比較すると、(\(x\)軸方向の\(\phi\)の微小変化と\(y\)軸方向の\(\phi\)の微小変化とが同じとき)\begin{eqnarray}E_x~\partial x&=&E_y~\partial y\nonumber\\ \frac{E_x}{\partial y}&=&\frac{E_y}{\partial x}\nonumber\end{eqnarray}各軸方向の電界\(E_x,~E_y\) の微小変化の変化率が同じであるとき、\[\frac{\partial E}{\partial y}=\frac{\partial E_y}{\partial x}\]となる(要確認?)。
p195 \(\int_s\vec{T_x}\cdot\vec{n} dS\)
ガウスの発散定理(p91)より、\begin{eqnarray}\int_S\vec{T_x}\cdot\vec{n} dS&=&\int_V\mathrm{div}\vec{T_x}~dV\nonumber\\&=&\int_V\left(\frac{\partial T_{xx}}{\partial x}+\frac{\partial T_{xy}}{\partial y}+\frac{\partial T_{xz}}{\partial z}\right)dV\nonumber\\&=&\int_V\left[\frac{1}{\mu_0}\left\{\left(\frac{\partial B_x}{\partial z}-\frac{\partial B_z}{\partial x}\right)B_z-\left(\frac{\partial B_y}{\partial x}-\frac{\partial B_x}{\partial y}\right)B_y\right\}\right]dV\nonumber\end{eqnarray}同式の括弧内が、ベクトル積\begin{eqnarray}\vec{i}\times\vec{B}&=&\frac{1}{\mu_0}\mathrm{rot}\vec{B}\times \vec{B}\nonumber\\&=&\left(\begin{array}{c}\frac{1}{\mu_0}\left\{\left(\frac{\partial B_x}{\partial z}-\frac{\partial B_z}{\partial x}\right)B_z-\left(\frac{\partial B_y}{\partial x}-\frac{\partial B_x}{\partial y}\right)B_y\right\}\\ \cdots \\ \cdots \end{array}\right)\nonumber\end{eqnarray}の1行目と等しいので(末尾4~2行目)、これを、\[\left(\vec{i}\times\vec{B}\right)_1\]と表すと(p177の表現方式)、与式は、\[\int_S\vec{T_x}\cdot\vec{n} dS=\int_V\left(\vec{i}\times\vec{B}\right)_1dV\]となる。
同様に、\(\int_s\vec{T_y}\cdot\vec{n} dS\) や \(\int_S\vec{T_z}\cdot\vec{n} dS\) についても、\[\int_S\vec{T_y}\cdot\vec{n} dS=\int_V\left(\vec{i}\times\vec{B}\right)_2dV\]\[\int_S\vec{T_z}\cdot\vec{n} dS=\int_V\left(\vec{i}\times\vec{B}\right)_3dV\]となる。これら3式を、\(T^m\) に関する式としてまとめると、\begin{eqnarray}\int_S T^m\vec{n} dS&=&\int_S\left(\begin{array}{c}\vec{T_x}\cdot\vec{n}\\ \vec{T_y}\cdot\vec{n}\\ \vec{T_z}\cdot\vec{n}\end{array}\right)dS\nonumber\\&=&\int_V\left(\begin{array}{c}\left(\vec{i}\times\vec{B}\right)_1\\ \left(\vec{i}\times\vec{B}\right)_2\\\left(\vec{i}\times\vec{B}\right)_3 \end{array}\right)dV\nonumber\\&=&\int_V\vec{i}\times\vec{B}~dV\nonumber\end{eqnarray}
p196 \(\vec{i}\times\vec{B}\) は、単位体積当たりローレンツ力
電荷密度 \(\rho~\left[\frac{Q}{m^3}\right]\)、電荷の速度 \(\vec{v}~\left[\frac{m}{s}\right]\) として、電流密度\(\vec{i}~\left[\frac{Q}{m^2\cdot s}\right]\) は、\[\vec{i}=\rho \vec{v}\]他方で、ローレンツ力 \(\vec{F}\) は、電荷を\(q\) とすると、\[F=q\vec{v}\times \vec{B}\]である(p181)。
よって、体積あたりのローレンツ力を \(\vec{f}\) 、体積を\(V~[m^3]\)とすると、\begin{eqnarray}\vec{f}&=&\frac{F}{V}\nonumber\\&=&\frac{q}{V}\vec{v}\times\vec{B}\nonumber\\&=&\rho\vec{v}\times\vec{B}\nonumber\end{eqnarray} であるので、\begin{eqnarray}\vec{i}\times\vec{B}&=&\rho\vec{v}\times\vec{B}\nonumber\\&=&\vec{f}\nonumber\end{eqnarray}となる。
これを体積積分した\[\int_V\vec{f}~dV\]は、領域\(V\) が磁場から受けるローレンツ力 \(\vec{F}\) を示している。
p196 静電場のエネルギー密度
静電場のエネルギー密度は、p167 のとおり、\[\frac{1}{2}\varepsilon_0E^2\]ここで、電束密度の大きさ \(D\) は、\(D=\varepsilon_0E\)であり(p155)、そのベクトル \(\vec{D}\)の方向は、電界ベクトル \(\vec{E}\) の方向と同じであるから、\begin{eqnarray}\frac{1}{2}\varepsilon_0E^2&=&\frac{1}{2}\varepsilon_0E\frac{D}{\varepsilon_0}\nonumber\\&=&\frac{1}{2}ED\nonumber\\&=&\frac{1}{2}|E||D|\cos0\nonumber\\&=&\frac{1}{2}\vec{E}\cdot\vec{D}\nonumber\end{eqnarray}として、両ベクトルの内積として表現できる。
p196 静磁場のエネルギー密度
静磁場のエネルギー密度は、p190 のとおり、\[\frac{1}{2\mu_0}B^2\]ここで、磁束密度の大きさ \(B\) は、\(B=\mu_0H\)であり(p171)、そのベクトル \(\vec{B}\)の方向は、磁界ベクトル \(\vec{H}\) の方向と同じであるから、\begin{eqnarray}\frac{1}{2\mu_0}B^2&=&\frac{1}{2\mu_0}B\mu_0H\nonumber\\&=&\frac{1}{2}BH\nonumber\\&=&\frac{1}{2}|B||H|\cos0\nonumber\\&=&\frac{1}{2}\vec{B}\cdot\vec{H}\nonumber\end{eqnarray}として、両ベクトルの内積として表現できる。
p197 \(\frac{\vec{E}\cdot\vec{D}}{2}\) の時間微分
\begin{eqnarray}\frac{\partial}{\partial t}\frac{\vec{E}\cdot\vec{D}}{2}&=&\frac{\partial}{\partial t}\left(\frac{\vec{E}\cdot\varepsilon\vec{E}}{2}\right)\nonumber\\&=&\frac{\varepsilon}{2}\frac{\partial}{\partial t}\left(\vec{E}\cdot\vec{E}\right)\nonumber\\&=&\frac{\varepsilon}{2}\frac{\partial}{\partial t}\left\{\left(\begin{array}{c}E_x\\E_y\\E_z\end{array}\right)\cdot\left(\begin{array}{c}E_x\\E_y\\E_z\end{array}\right)\right\}\nonumber\\&=&\frac{\varepsilon}{2}\frac{\partial}{\partial t}\left(E_x^2+E_y^2+E_z^2\right)\nonumber\end{eqnarray}
ここで、\(\frac{\partial}{\partial t}E_x^2\) について、ライプニッツ則(p26)を用いると、\begin{eqnarray}\frac{\partial}{\partial t}E_x^2&=&E_x\frac{\partial E_x}{\partial t}+\frac{\partial E_x}{\partial t}E_x\nonumber\\&=&2E_x\frac{\partial E_x}{\partial t}\nonumber\end{eqnarray}\(\frac{\partial}{\partial t}E_y^2\) や \(\frac{\partial}{\partial t}E_z^2\) についても同様に考えられるので、 与式は、\begin{eqnarray}\frac{\partial}{\partial t}\frac{\vec{E}\cdot\vec{D}}{2}&=&\frac{\varepsilon}{2}\left(2E_x\frac{\partial E_x}{\partial t}+2E_y\frac{\partial E_y}{\partial t}+2E_z\frac{\partial E_z}{\partial t}\right)\nonumber\\&=&\varepsilon\left(E_x\frac{\partial E_x}{\partial t}+E_y\frac{\partial E_y}{\partial t}+E_z\frac{\partial E_z}{\partial t}\right)\nonumber\end{eqnarray}となる。
他方で、\begin{eqnarray}\vec{E}\cdot\frac{\partial\vec{D}}{\partial t}&=&\left(\begin{array}{c}E_x\\E_y\\E_z\end{array}\right)\cdot\left(\begin{array}{c}\frac{\partial}{\partial t}\varepsilon E_x\\ \frac{\partial}{\partial t}\varepsilon E_y\\ \frac{\partial}{\partial t}\varepsilon E_z\end{array}\right)\nonumber\\&=& \varepsilon \left(E_x\frac{\partial E_x}{\partial t}+E_y\frac{\partial E_y}{\partial t}+E_z\frac{\partial E_z}{\partial t} \right)\nonumber\end{eqnarray}よって、\[\frac{\partial}{\partial t}\frac{\vec{E}\cdot\vec{D}}{2}=\vec{E}\cdot\frac{\partial\vec{D}}{\partial t}\]と言える。
これは、ベクトル\(\vec{E},~\vec{D}\) をスカラー値とみたてて微分したものと、結果的に一致する。
p197 \(\frac{\vec{B}\cdot\vec{H}}{2}\) の時間微分
ベクトル \(\vec{B},~\vec{H}\) をスカラー値とみたてて微分すると、\begin{eqnarray}\frac{\partial}{\partial t}\frac{\vec{B}\cdot\vec{H}}{2}&=&\frac{1}{2}\frac{\partial}{\partial t}\left(\vec{B}\cdot\vec{H}\right)\nonumber\\&=&\frac{1}{2}\frac{\partial}{\partial t}\left(\vec{B}\cdot\frac{1}{\mu}\vec{B}\right)\nonumber\\&=&\frac{1}{2\mu}\frac{\partial}{\partial t}\left(\vec{B}\cdot\vec{B}\right)\nonumber\\&=&\frac{1}{2\mu}\left(\vec{B}\cdot\frac{\partial\vec{B}}{\partial t}+\frac{\partial\vec{B}}{\partial t}\cdot\vec{B}\right)\nonumber\\&=&\frac{1}{2\mu}\left(2\vec{B}\cdot\frac{\partial \vec{B}}{\partial t}\right)\nonumber\\&=&\frac{\vec{B}}{\mu}\cdot\frac{\partial \vec{B}}{\partial t}\nonumber\\&=&\vec{H}\cdot\frac{\partial\vec{B}}{\partial t}&\nonumber\end{eqnarray}と変形可能である。
p197 末尾4行目~3行目
ガウスの発散定理(p91)を用いて、\[\int_V\mathrm{div}\left(\vec{E}\times\vec{H}\right)dV=\int_S\left(\vec{E}\times\vec{H}\right)\cdot\vec{n}~dS\]と変形している。
§11 マックスウェルの方程式をポテンシャルで書き換え
p205 \(\rho,~\vec{i},~\phi,~\vec{A},~\vec{B},~\vec{E}\)
位置\(\vec{x}\)、時間\(t\) で定まる電荷密度 \(\rho\) と電流密度 \(\vec{i}\) により、電界 \(\vec{E}\) と磁束密度 \(\vec{B}\) とが求められる。
- 電荷密度 \(\rho\)
- 電流密度 \(\vec{i}\)
- スカラーポテンシャル \(\phi\)
- ベクトルポテンシャル \(\vec{A}\)
- 電界 \(\vec{E}\)
- 磁束密度 \(\vec{B}\)
ローレンツ・ゲージ条件は、\[\mathrm{div}\vec{A}+\varepsilon_0\,u_0\frac{\partial \phi}{\partial t}=0\]