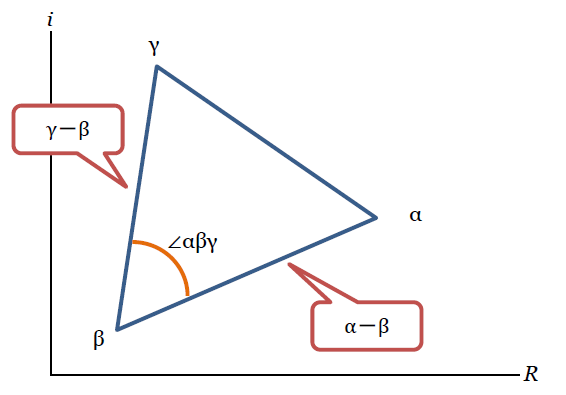
理工系のための経済学・ファイナンス理論
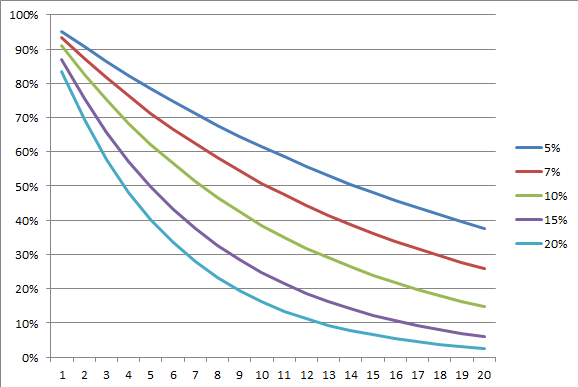
縄田和満著「理工系のための経済学・ファイナンス理論」東洋経済新報社(2003/3/1) https://www.amazon.co.jp//dp/4492313230 p192 ベルヌーイ試行、2項分布 \[f(x)={}_nC_xp^x(1-p)^{n-x} \]反復試行の確率(なかけんの数学ノート) https://math.nakaken88.com/textbook/basic-probability-of-repeated-trials/ p200 10行目 (誤)連続型の場合にはそれらの確率関数は、 (正)離散型の場合にはそれらの確率関数は、 p200 式(13.22) (誤)\(\displaystyle g(x)=\sum_x f(x,y),~~h(y)=\sum_y f(x,y)\) (正)\(\displaystyle g(x)=\sum_y f(x,y),~~h(y)=\sum_x f(x,y)\) p206 割引率 利子率\(r=5%,~7%,~10%,~15%,~20%\) と将来年数\(t\) による割引率 p207 収益が一定の場合の現在価値 初期投資 \(C=100\)、プロジェクト期間 \(T=20\)、利子率 \(r=5\%\)、各年の収益は一定値 \(A=10\) の場合、現在価値は、\begin{eqnarray}PV&=&V-C\nonumber\\&=&124.62-100\nonumber\\&=&24.62\nonumber\end{eqnarray} プロジェクト期間15年後から、現在価値 \(PV\) は+に転じる。 p207 5行目 (誤)プロジェクトを行う (正)プロジェクトを行うことが有益となるのは p207 末尾1行目 (誤)\(PV=C-V=24.62\) (正)\(PV=V-C=24.62\) p208 式(14.11) から (14.12) の変形 \begin{eqnarray}A_{t+1}&=&(1+r)A_t-R\nonumber\\A_{t+1}-\frac{R}{r}&=&(1+r)A_t-R-\f