「入門 信頼性工学」第3章~第4章
福井泰好「入門 信頼性工学(第2版)」森北出版 の読後メモ。
設例について、Python [Google Colaboratory]による演算処理例を示す。
3章 信頼性工学の概要
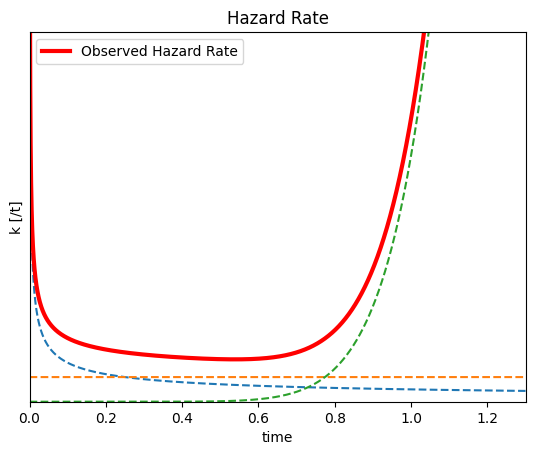
p47 図3.6 故障率λ
(処理手順)
- ワイブル式より、DFR・CFR・IFRの各分布を計算
- 上記分布を合算(観測される故障率λの分布)
(コード)
故障率kのグラフ と同じ
- 赤色実線:観測される故障率λ曲線(バスタブ曲線)
- 青色点線:DFR分布
- 橙色点線:CFR分布
- 赤色点線:IFR分布
p47 図3.6 確率密度f
(処理手順)
- 赤色実線:観測される確率密度f曲線
- 青色点線:DFR分布
- 橙色点線:CFR分布
- 赤色点線:IFR分布
p47 図3.6 信頼度R
(処理手順)
- 赤色実線:観測される信頼度R曲線
- 青色点線:DFR分布
- 橙色点線:CFR分布
- 赤色点線:IFR分布
p52 例題3.1(1) 総試験時間 定数打切り方式
(処理手順)
- 寿命試験結果のデータを設定
- 同データを、指定個数分(故障が発現済み)/未発現に区分
- 故障が発現済み:寿命時間を加算
- 故障が未発現:指定個数の最長寿命 × 未発現データ個数
- 各区分の計算結果を合算
time_list = [45,53,55,61,65,67,70,71,74,75] # 寿命試験結果
f_num = 4 # 故障数
t_list = sorted(time_list) # 昇順に並び替え
# 故障が発現済み
confirmed = t_list[:f_num]
con_sum = sum(confirmed)
# 故障が未発現
residual = len(t_list)-len(confirmed)
res_sum = confirmed[-1] * residual
# 総試験時間Tc
total = con_sum + res_sum
print(f'定数打切り方式(故障数{f_num}個)での総試験時間Tr:{total}[時間]')
定数打切り方式(故障数4個)での総試験時間Tr:580[時間]
p52 例題3.1(2) 総試験時間 定時打切り方式
(処理手順)
- 寿命試験結果のデータを設定
- 同データを、定時までに故障が発現済み/未発現に区分
- 故障発現済み:寿命時間を加算
- 故障未発現:打切り時刻 × 未発現データ個数
- 各区分の計算結果を合算
# コードは上記の続き
f_time = 60 # 故障数
# 故障が発現済み
confirmed = [time for time in t_list if time < f_time]
con_sum = sum(confirmed)
# 故障が未発現
residual = len(t_list)-len(confirmed)
res_sum = f_time * residual
# 総試験時間Tc
total = con_sum + res_sum
print(f'定時打切り方式(打切時間{f_time}時間)での総試験時間Tc:{total}[時間]')
定時打切り方式(打切時間60時間)での総試験時間Tc:573[時間]
p53 時間推移
- Mean Time to Failure
- Mean Operating Time = Mean Time Between Failures
- Mean Time to First Failure
- Mean Up Time
- Mean Down Time
- Mean Time to Repair
p53 例題3.2 MTTF
(処理工程)
- 寿命データを設定
- 寿命の合計値 ÷ 寿命データ個数 =MTTF
t_list = [45,53,55,61,65,67,70,71,74,75] # 寿命試験結果
mttf = sum(t_list)/len(t_list)
print(f'MTTF:{mttf}時間')
MTTF:63.6時間
p54 例題3.3 MTBF
(処理工程)
- 故障時刻データを設定
- 故障時刻データの差分を計算 →故障間隔
- 故障間隔 ÷ データ個数 =MTBF
t_list = [20,45,75,100] # 故障時刻
ele_num = len(t_list) # 個数
t_list.insert(0, 0) # 冒頭時刻を追加
dif = [i-j for i, j in zip(t_list[1:], t_list[:-1])] # 運用後故障間隔
mtbf = sum(dif)/ele_num
print(f'MTBF:{mtbf}時間')
MTBF:25.0時間
p54 例題3.4 MTTFF
(処理工程)
- 運用結果データを設定
- 合計値 ÷ データ数 =MTTFF
t_list = [7,8,9] # 運用結果
mttf = sum(t_list)/len(t_list)
print(f'MTTFF:{mttf}時間')
MTTFF:8.0時間
p54 例題3.5 MTTR
(処理工程)
- 時間データ、個数データを設定
- 時間データと個数データを1対にする(辞書型)
- 時間と個数を乗算
- 同乗算データを合計 →MTTR
time = [1,2,3,4,5,6,7]
num_m = [15,10,7,3,1,1,2]
r_num = dict(zip(time,num_m))
# 補修時間×個数
t_n = 0
for rep in r_num.keys():
t_n += rep * r_num[rep]
# 表示
print(f'MTTR:{round(t_n/sum(num_m),3)}時間')
MTTR:2.385時間
p56 演習問題3.1
(処理工程)
- 確率密度、監視時刻を設定
- 次回監視迄の残時間計算式を設定
- 各監視時刻間帯域における残時間を表記
- 残時間計算式を、各監視時刻間帯域にて定積分
- 上記定積分の結果を合計
(使用モジュール)
- 計算式の文字数処理:sympy の Symbols
- 定積分:sympy の integrate
from sympy import *
# 設定値
fx = 1/60 # 確率密度
spots = [0,15,35,60] # 監視時刻
# 区間の上下限リスト
upper = spots[1:]
lower = spots[:-1]
# 次回監視までの残時間
x = Symbol('x')
t_value = [time -x for time in upper]
print(f'不具合時刻x秒のとき、次回監視までの残時間t秒')
for num in range(len(spots)-1):
print(f'・xが{lower[num]}~{upper[num]} 秒のとき:t= {t_value[num]} 秒')
# 期待値
expected60 = 0
for number in range(len(spots)-1):
element = integrate(t_value[number], (x,lower[number], upper[number]))
expected60 += element
print(f'期待値:{round(expected60 *fx,2)}秒')
不具合時刻x秒のとき、次回監視までの残時間t秒 ・xが0~15 秒のとき:t= 15 - x 秒 ・xが15~35 秒のとき:t= 35 - x 秒 ・xが35~60 秒のとき:t= 60 - x 秒 期待値:10.42秒
p56 演習問題3.2(1)
(処理工程)
- 二次関数の一般式を設定
- 既知解を与えて、定数a,b,c を求める
- 求めた確率密度関数を表示する
(使用モジュール)
- 計算式の文字数処理:sympy の var
- 方程式の解法:sympy の solve
import sympy
from sympy import *
sympy.var('x, a, b, c')
function = a*x**2 +b*x +c # 二次関数の一般式
# 設定値
x_sub0,f0value = 0,0 # f(0)=0
x_sub1,f1value = 1,0 # f(1)=0
x_subL,x_subU ,f01value = 0,1,1 # ∫f(0~1)=1
# f(0)=0 条件で、c を求める
fx0 = function.subs([(x, x_sub0)])
c_value = sympy.solve (fx0-f0value, c)
print(f'f({x_sub0})=0 より、c={c_value[0]}')
# f(1)=0 条件で、b を求める
fx1 = function.subs([(x, x_sub1),(c,c_value[0])])
b_value = sympy.solve (fx1-f1value, b)
print(f'f({x_sub1})=0 より、b={b_value[0]}')
# ∫f(0~1)=1 の条件で、a を求める
fx2 = function.subs([(c,c_value[0]),(b,b_value[0])])
a_value = sympy.solve (integrate(fx2,(x,x_subL,x_subU))-f01value,a)
print(f'f({x_subL}~{x_subU})={f01value} より、a={a_value[0]}')
# 確率密度関数f(x)
fx = function.subs([(c,c_value[0]),(b,b_value[0]),(a,a_value[0])])
print(f'よって、確率密度関数f(x)は、')
sympy.init_printing()
display(fx)
p56 演習問題3.2(2)
(処理工程)
- 確率密度関数f(x) から、期待値を求める
- 確率密度関数f(x) から、分散値を求める
(使用モジュール)
# コードは上記の続き
# 期待値
expected = integrate(x*fx,(x,0,1))
print(f'期待値:{float(expected)}')
# 分散
var = integrate((x-expected)**2*fx,(x,0,1))
print(f'分散:{float(var)}')
期待値:0.5 分散:0.05
p56 演習問題3.3 MTTF
(処理工程)
- p53 例題3.2 MTTFと同様
t_list = [300,350,400,450,500] # 寿命試験結果
mttf = sum(t_list)/len(t_list)
print(f'MTTF:{mttf}時間')
MTTF:400.0時間
p56 演習問題3.4 MTBF
(処理工程)
- p54 例題3.3 MTBFと同様
t_list = [200,405,705,960,1200] # 故障時刻
ele_num = len(t_list) # 個数
t_list.insert(0, 0) # 冒頭時刻を追加
dif = [i-j for i, j in zip(t_list[1:], t_list[:-1])] # 運用後故障間隔
mtbf = sum(dif)/ele_num
print(f'MTBF:{mtbf}時間')
MTBF:240.0時間
p56 演習問題3.5 MTTR
(処理工程)
- p54 例題3.5 MTTRと同様
time = [5,10,15,20,25,30,40,60]
num_m = [1,6,3,8,4,5,2,1]
r_num = dict(zip(time,num_m))
# 補修時間×個数
t_n = 0
for rep in r_num.keys():
t_n += rep * r_num[rep]
# 表示
print(f'MTTR:{round(t_n/sum(num_m),3)}分')
MTTR:22.0分
4章 信頼評価関数の基礎
p58 図4.1 二項分布
(処理工程)
- 二項分布の確率関数 \(f(x)=_nC_x p^x(1-p)^{n-x}\) を設定
- 全ての確率p、出現数x について上記関数で確率を計算
- グラフ化
from matplotlib import pyplot as plt
import numpy as np
import math
# 設定値
number = 10 # サンプル数
p_list = np.arange(0.1, 1, 0.2) # 確率
x_list = np.arange(11) # 出現数
# 関数 二項分布
def fx(snum,prob,xs):
return math.comb(snum,xs) * prob**xs *(1-prob)**(snum-xs)
# グラフ化
for proba in p_list: # 各確率について
fx_list =[]
for xvalue in x_list: # 各出現回数について
fx_list.append(fx(number,proba,xvalue)) # 二項分布確率をリスト化
plt.plot(x_list,fx_list,label=f'p={round(proba,2)}')
# 凡例
plt.xlabel('Number of Occurrences of Event [x]')
plt.ylabel('Probability of Appearance [y]')
plt.title(f'Sample Number={number}')
plt.legend()
plt.show()
p59 例題4.1(1) 不良品の個数がある値となる確率
(処理手順)
- 関数(二項分布)を設定
- 母集団の不良率、標本の個数、標本中の不良品数を設定
- 同関数を使用して、確率を計算
import math
# 設定値
p_frate = 0.05 # 母集団の不良率
s_num = 10 # 標本の個数
s_fail = 3 # 標本中の不良品数
# 関数 二項分布
def fx(snum,rate,xs):
return math.comb(snum,xs) * rate**xs *(1-rate)**(snum-xs)
# 演算と表示
prob_01 = fx(s_num, p_frate, s_fail)
print(f'母集団不良率{round(p_frate*100)}%のとき、標本{s_num}個中に不良品個数{s_fail}個となる確率は、{round(prob_01*100,3)}%')
母集団不良率5%のとき、標本10個中に不良品個数3個となる確率は、1.048%
p59 例題4.1(2) 不良品の個数がある値以下となる確率
(処理手順)
- 関数(二項分布の確率)を設定
- 標本中の不良品数の上限を設定
- 各不良品数の確率を上記関数で計算
- 各不良品数を生ずる事象の確率を合計する(=不良品上限以下となる事象確率)
# コードは上記の続き
s_fail_up = 2 # 標本中の不良品数の上限
# 標本中不良品数の上限まで確率を積算
prob_02 = 0
for sf in range(s_fail_up+1):
prob_02 += fx(s_num, p_frate, sf)
# 表示
print(f'母集団不良率{round(p_frate*100)}%のとき、標本{s_num}個中に不良品個数{s_fail_up}個以下となる確率は、{round(prob_02*100,3)}%')
母集団不良率5%のとき、標本10個中に不良品個数2個以下となる確率は、98.85%
p60 二項分布とポアソン分布(n=10)
(処理手順)
- 標本数n、母集団不良率pを設定
- 平均 μ=np を計算
- 二項分布のグラフを描画(複数の p)
- ポアソン分布のグラフを描画(複数の μ)
from matplotlib import pyplot as plt
import numpy as np
import math
# 設定値
number = 10 # サンプル数
p_list = [0.1, 0.5] # 確率
x_list = np.arange(number+5) # 出現数
myu_list = [number *p_value for p_value in p_list] # 平均値
# 関数 二項分布
def fx(snum,prob,xs):
return math.comb(snum,xs) * prob**xs *(1-prob)**(snum-xs)
# 関数 ポアソン分布
def Poisson(myu,xs):
return myu**xs /math.factorial(xs) *math.exp(-myu)
# 二項分布をグラフ化
for proba in p_list: # 各確率について
fx_list =[]
for xvalue in x_list: # 各出現回数について
fx_list.append(fx(number,proba,xvalue)) # 二項分布確率をリスト化
plt.plot(x_list,fx_list,label=f'p={round(proba,2)}')
# ポアソン分布をグラフ化
for myu in myu_list: # 各平均について
fx_list =[]
for xvalue in x_list: # 各出現回数について
fx_list.append(Poisson(myu,xvalue)) # ポアソン分布確率をリスト化
plt.plot(x_list,fx_list,"--", label=f'μ={round(myu,2)}')
# 凡例
plt.xlabel('Number of Occurrences of Event [x]')
plt.ylabel('Probability of Appearance')
plt.title(f'binomial distribution, SN={number}')
plt.legend()
plt.show()
- 実線:二項分布
- 破線:ポアソン分布
p60 二項分布とポアソン分布(n=100)
サンプル数を100へと増加した例(上記コードで、number = 10 を、number = 100 へと変更した場合)
- サンプル数を大きくすると(n=10 →100)、小さいp(小さい μ)について、近似度が高まる。
- サンプル数を大きくしても、大きなp(大きい μ)では、近似度は低い。
p61 図4.2 ポアソン分布の確率関数
(処理手順)
- 関数(ポアソン分布の確率分布)を設定
- 平均値、出現数のリストを設定
- 上記関数で確率リストを生成
- グラフ化
import numpy as np
import math
from matplotlib import pyplot as plt
# 設定値
myu_list = [0.1,0.5,1,3,5,8,10] # 平均値
x_list = np.arange(11) # 出現数
# 関数 ポアソン分布
def Poisson(myu,xs):
return myu**xs /math.factorial(xs) *math.exp(-myu)
# グラフ化
for myu in myu_list: # 各平均について
fx_list =[]
for xvalue in x_list: # 各出現回数について
fx_list.append(Poisson(myu,xvalue)) # ポアソン分布確率をリスト化
plt.plot(x_list,fx_list,label=f'μ={round(myu,2)}')
# 凡例
plt.xlabel('Number of Occurrences of Event [x]')
plt.ylabel('Probability of Appearance')
plt.title(f'Poisson Distribution')
plt.legend()
plt.show()
p61 例題4.2 3件以上の故障が発生する確率(余事象による計算)
(処理手順)
- 平均故障数を設定
- 故障数の下限を設定
- 関数(ポアソン分布)を設定
- 同関数で、故障数の下限未満の事象を逐次計算
- 故障数の下限未満の事象の確率を合計
- 全体確率 - 余事象(故障数の下限未満の事象)確率 =設定故障数以上となる確率
import numpy as np
import math
# 設定値
myu = 24/60 # 平均故障数[個/月]
x_under = 3 # 出現数の下限
# 関数 ポアソン分布
def Poisson(myu,xs):
return myu**xs /math.factorial(xs) *math.exp(-myu)
# 出現数の下限未満の事象確率
fx_list = [] # 各個数が生じる確率のリスト
for xs in range(x_under): # 0~出現数未満について
fx_list.append(Poisson(myu,xs)) # ポアソン分布確率をリスト化
# 余事象の確率
prob = 1-sum(fx_list) # 出現数以上となる確率
print(f'1か月あたり{x_under}件以上の故障が発生する確率:{round(prob*100,4)}%')
1か月あたり3件以上の故障が発生する確率:0.7926%
p61 連続型確率分布
- 指数分布:故障率λが時間tに依存しない(偶発故障)期間の分布。
- 正規分布:多数部品からなるアイテムの故障分布。
- 対数正規分布:材料の破壊寿命分布、機器の修理時間分布・保全時間、機械の実働加重頻度分布、電子部品の故障分布
- ワイブル分布:金属材料の疲労寿命
p63 図4.3 指数分布
(処理工程)
- 指数分布の確率密度関数 \(f(t)=\lambda e^{-\lambda t}\) を設定
- リストの全時刻\(t\)、全故障率\(\lambda\) について上記関数で確率を計算
- グラフ化
import numpy as np
import math
from matplotlib import pyplot as plt
time_list = np.arange(0,6,0.1)
lambda_list = [0.5, 0.8, 1, 1.5]
# 確率 確率密度f(t)
def fx(lamb,time):
return lamb * math.exp(-lamb *time)
# グラフを描画
for lamb in lambda_list:# 全てのλについて
fx_list = []
for time in time_list: # 全ての時間について
fx_list.append(fx(lamb, time))
plt.plot(time_list,fx_list,label=f'λ={lamb}')
# 凡例等
plt.legend()
plt.xlabel('time')
plt.ylabel('f(t)')
plt.title('Exponential Distribution')
plt.xlim(0,)
plt.ylim(0,)
plt.show()
p63 図4.4 指数分布の平均t=μと信頼度R(t)
import numpy as np
import math
from matplotlib import pyplot as plt
# 設定値
time_list = np.arange(0,6,0.1)
lamb = 0.8
# 確率 確率密度f(t)
def fx(lamb,time):
return lamb * math.exp(-lamb *time)
# 確率密度グラフを描画
fx_list = []
for time in time_list: # 全ての時間について
fx_list.append(fx(lamb, time))
plt.plot(time_list,fx_list)
# t=平均μでのグラフ区分
myu = 1/lamb # 平均μ
y_myu = fx(lamb,myu)
plt.vlines(myu,0,y_myu)
# 塗りつぶし
Ysq = np.linspace(0,0,60) # 0から0まで60個のリスト(y=0 のデータ)
plt.fill_between(time_list, fx_list, Ysq, where=(time_list>=0),fc= 'lightgrey')
plt.fill_between(time_list, fx_list, Ysq, where=(time_list>=myu),fc= 'lightblue')
# 凡例等
plt.xlabel('time')
plt.ylabel('f(t)')
plt.title('Exponential Distribution')
plt.xlim(0,)
plt.ylim(0,)
plt.xticks([myu],[r'$ \mu $' ]) # x軸目盛
plt.yticks([])
plt.show()
青色部分:\(R(t)\) 信頼度関数の値
p63 例題4.3 指数分布 故障率λ
式4.12 を\(\lambda\) について解くと、
\begin{eqnarray*}R(t)&=&e^{-\lambda t} \\log_e R(t)&=& log_e e^{-\lambda t} \\ &=& -\lambda t\\ \lambda &=& -\cfrac{log_e R(t)}{t}\end{eqnarray*}
(使用モジュール)
- 対数:math.log
import math
time =1000
Rel = 0.95
def R_lamb(Rel,time):
return -math.log(Rel)/time
lamb = R_lamb(Rel,time)
print(f'故障率:{lamb}[/時間]')
故障率:5.1293294387550576e-05[/時間]
p66 図4.5(a) 正規分布の確率密度関数 f(x)
(使用モジュール)
- 正規分布の確率密度関数(Probability Density Function):scipy.stats.norm.pdf
from matplotlib import pyplot as plt
from scipy.stats import norm
import numpy as np
myu = 0 # 平均
std_list = [0.5, 1, 2.0] # 分散
x_list = np.arange(-3,3,0.01)
for std in std_list: # 全ての分散について
fx_list = []
for x_value in x_list:
fx_list.append(norm.pdf(x_value, loc=myu, scale=std))
plt.plot(x_list,fx_list,label=f'σ={std}')
plt.xlim(-3,)
plt.ylim(0,)
plt.legend()
plt.xlabel('x')
plt.ylabel('f(x)')
plt.title('Probability Density [Normal Dist.]')
plt.show()
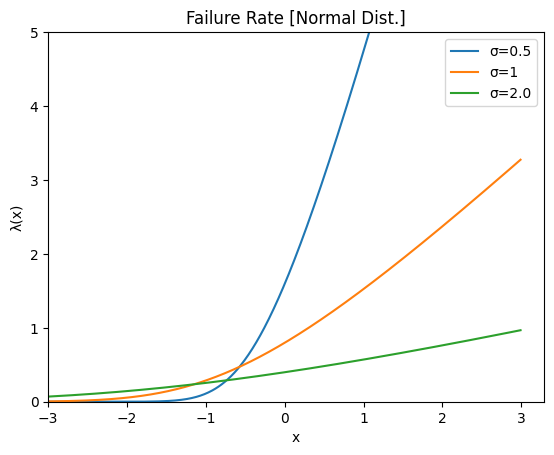
p66 図4.5(b) 正規分布の故障率関数λ(x)
(処理工程)
- 確率密度関数\(f(x)\) ÷ 信頼度関数\(R(x)\) =故障率関数 \(\lambda(x)\)
- 故障率関数を用いて、各\(x\) について、故障率を計算
- 所定の分散について、同計算を実施
- グラフ化
# コードは上記の続き
# 関数 ガンマ関数
def norm_gamma(x_value,myu,std):
fx = norm.pdf(x_value, loc=myu, scale=std) # 確率密度の関数
Rx = 1-norm.cdf(x_value, loc=myu, scale=std) # 信頼度の関数
return fx/Rx
for std in std_list: # 全ての分散について
sigma_list = []
for x_value in x_list:
sigma_list.append(norm_gamma(x_value, myu, std))
plt.plot(x_list,sigma_list,label=f'σ={std}')
# 凡例
plt.xlim(-3,)
plt.ylim(0,5)
plt.legend()
plt.xlabel('x')
plt.ylabel('λ(x)')
plt.title('Failure Rate [Normal Dist.]')
plt.show()
p66 例題4.4 正規分布 アイテム寿命時間
(処理工程)
- 平均、分散、下限時間を設定
- 下限時間を変数\(t\)に標準化
- 変数\(t\) に対応する正規分布の左側確率を求める
- 全確率1-左側確率 =右側確率
(使用モジュール)
- \(\sqrt{}\) 計算:math.sqrt
- 正規分布の左側確率(Cumulative Distribution Function):scipy.stats.norm.cdf
from scipy.stats import norm
import math
# 設定値
myu = 100 # 平均
var = 25 # 分散
time_lower = 90 # 下限時間
sigma = math.sqrt(var) # 標準偏差
# 標準化
t_value = (time_lower - myu)/sigma
print(f'標準化変数t= {t_value}')
# 確率
rel = 1-norm.cdf(t_value)
print(f'アイテム寿命が{time_lower}時間以上となる確率:{round(rel*100,3)}%')
標準化変数t= -2.0 アイテム寿命が90時間以上となる確率:97.725%
p67 図4.6(a) 対数正規分布 確率密度関数
import numpy as np
import math
from scipy.stats import norm
from matplotlib import pyplot as plt
# 設定データ
myu_list = [0, 0, 1] # 平均
std_list = [1, 0.5, 0.5] # 分散
z_list = np.arange(0.01,4,0.01)
# 関数 対数正規分布の確率密度 f(z)
def log_norm(z_value, myu, std):
return 1/(std * z_value) * norm.pdf((math.log(z_value)-myu)/std)
# グラフ描画
for myu,std in zip(myu_list,std_list): # 全ての平均と分散について
fz_list = []
for z_value in z_list:
fz_list.append(log_norm(z_value,myu,std))
plt.plot(z_list,fz_list,label=f'μ_L={myu}, σ_L={std}')
# 凡例
plt.xlim(0,)
plt.ylim(0,1)
plt.legend()
plt.xlabel('z')
plt.ylabel('f(z)')
plt.title('Probability Density [Log-Normal Dist.]')
plt.show()
p67 図4.6(b) 対数正規分布 故障率関数
# コードは上記の続き
# 関数 ガンマ関数
def log_norm_gamma(z_value,myu,std):
fz = log_norm(z_value, myu, std) # 確率密度の関数
Rz = norm.cdf((myu - math.log(z_value))/std) # 信頼度の関数
return fz/Rz
for myu,std in zip(myu_list,std_list): # 全ての平均と分散について
gamma_list = []
for z_value in z_list:
gamma_list.append(log_norm_gamma(z_value, myu, std))
plt.plot(z_list,gamma_list,label=f'μ_L={myu}, σ_L={std}')
plt.xlim(0,)
plt.ylim(0,2)
plt.legend()
plt.xlabel('x')
plt.ylabel('λ(x)')
plt.title('Failure Rate [Log Normal Dist.]')
plt.show()
p69 例題4.5 対数正規分布
from scipy.stats import norm
import math
# 設定値
myu_l = 5 # 平均
var_l = 1 # 分散
time = 100 # 指定時間
# 平均μ
myu = math.exp(myu_l +var_l/2)
print(f'期待値μ={round(myu,1)}[時間]')
# 標準偏差σ
left = math.exp(2 *myu_l + var_l)
right = math.exp(var_l)-1
std = math.sqrt(left*right)
print(f'標準偏差σ={round(std,1)}[時間]')
# 標準化t
t_value = (math.log(time) - myu_l)/math.sqrt(var_l)
print(f'標準化変数t= {round(t_value,4)}')
# 確率
rel = 1-norm.cdf(t_value)
print(f'運用時間{time}時間における信頼度R:{round(rel*100,2)}[%]')
# 関数 対数正規分布の確率密度 f(z)
def log_norm(z_value, myu_l, std_l):
return 1/(std_l * z_value) * norm.pdf((math.log(z_value)-myu_l)/std_l)
# 故障率λ
fz = log_norm(time,myu_l,math.sqrt(var_l)) # 確率密度
lambda_value = fz/rel
print(f'運用時間{time}時間における故障率λ:{round(lambda_value*100,4)}[%/時間]')
期待値μ=244.7[時間] 標準偏差σ=320.8[時間] 標準化変数t= -0.3948 運用時間100時間における信頼度R:65.35[%] 運用時間100時間における故障率λ:0.5647[%/時間]
p70 図4.7(a) ワイブル分布 確率密度関数
(処理工程)
- α、β、γのリストを設定
- ワイブル分布の関数を設定
- 各パラメータについてワイブル分布を計算
- グラフを描画
import numpy as np
import math
from matplotlib import pyplot as plt
# 設定データ
alpha_list = [0.5, 1, 2, 4] # 形状母数α
beta_list = [1,1,1,1] # 尺度母数β
t_list = np.arange(0.01,3,0.01)
# 関数 ワイブル分布の確率密度 f(t)
def Weibull(t_value, alpha, beta):
return alpha/beta * (t_value/beta)**(alpha-1) * math.exp(-(t_value/beta)**alpha)
# グラフ描画
for alpha,beta in zip(alpha_list,beta_list): # 全てのαとβについて
ft_list = []
for t_value in t_list:
ft_list.append(Weibull(t_value,alpha,beta))
plt.plot(t_list,ft_list,label=f'α={alpha}, β={beta}')
# 凡例
plt.xlim(0,)
plt.ylim(0,2)
plt.legend()
plt.xlabel('t')
plt.ylabel('f(t)')
plt.title('Probability Density [Weibull Dist.]')
plt.show()
p70 図4.7(b) ワイブル分布 故障確率関数
# コードは上記の続き
# 関数 λ関数
def Weibull_lambda(t_value,alpha,beta):
return (alpha * t_value**(alpha-1))/(beta**alpha)
for alpha,beta in zip(alpha_list,beta_list): # 全ての平均と分散について
lambda_list = []
for t_value in t_list:
lambda_list.append(Weibull_lambda(t_value, alpha, beta))
plt.plot(t_list,lambda_list,label=f'α={alpha}, β={beta}')
plt.xlim(0,)
plt.ylim(0,4)
plt.legend()
plt.xlabel('t')
plt.ylabel('λ(t)')
plt.title('Failure Rate [Weibull Dist.]')
plt.show()
p72 例題4.6 ワイブル分布
from scipy.special import gamma
import math
# 設定値
alpha = 5 # 形状
beta = 150 # 尺度
time = 100 # 指定時間
# 平均μ
myu = beta * gamma(1+1/alpha)
print(f'MTTF={round(myu,1)}[時間]')
# 標準偏差σ
left = gamma(1+2/alpha)
right = (gamma(1+1/alpha))**2
std = beta * math.sqrt(left - right)
print(f'標準偏差σ={round(std,2)}[時間]')
# 確率
rel = math.exp(-(time/beta)**alpha)
print(f'運用時間{time}時間における信頼度R:{round(rel*100,2)}[%]')
# 故障率λ
lambda_value = (alpha * time**(alpha-1))/(beta **alpha)
print(f'運用時間{time}時間における故障率λ:{round(lambda_value*100,4)}[%/時間]')
MTTF=137.7[時間] 標準偏差σ=31.55[時間] 運用時間100時間における信頼度R:87.66[%] 運用時間100時間における故障率λ:0.6584[%/時間]
p72 図4.8(a) 三母数ワイブル分布 確率密度関数
(処理工程)
- パラメータ α、β、γのリストを設定
- ワイブル分布の関数を設定(t<γのとき、値無しとする)
- 各パラメータについてワイブル分布を計算
- グラフを描画
import numpy as np
import math
from matplotlib import pyplot as plt
# 設定データ
alpha_list = [0.5, 1, 2, 4] # 形状母数α
beta_list = [1,1,1,1] # 尺度母数β
gamma_list = [0.2, 0.5, 1, 1.5]
t_list = np.arange(0.01,3,0.01)
# 関数 ワイブル分布(三母数)の確率密度 f(t)
def Weibull(t_value, alpha, beta, gamma):
if t_value > gamma:
ft = alpha/beta * ((t_value-gamma)/beta)**(alpha-1) * math.exp(-((t_value-gamma)/beta)**alpha)
else: # t_value < gammma のとき値なし
ft = None
return ft
# グラフ描画
for alpha,beta,gamma in zip(alpha_list,beta_list,gamma_list): # 全てのαβγについて
ft_list = []
for t_value in t_list:
ft_list.append(Weibull(t_value,alpha,beta,gamma))
plt.plot(t_list,ft_list,label=f'α={alpha}, β={beta},γ={gamma}')
# 凡例
plt.xlim(0,)
plt.ylim(0,2)
plt.legend()
plt.xlabel('t')
plt.ylabel('f(t)')
plt.title('Probability Density [Weibull_3parameters Dist.]')
plt.show()
p72 図4.8(b) 三母数ワイブル分布 故障確率関数
# コードは上記の続き
# 関数 ガンマ関数
def Weibull_lambda(t_value,alpha,beta,gamma):
if t_value > gamma:
lambda_value = alpha/beta * ((t_value-gamma)/beta)**(alpha-1)
else:
lambda_value = None
return lambda_value
for alpha,beta,gamma in zip(alpha_list,beta_list,gamma_list): # 全ての平均と分散と位置について
lambda_list = []
for t_value in t_list:
lambda_list.append(Weibull_lambda(t_value, alpha, beta, gamma))
plt.plot(t_list,lambda_list,label=f'α={alpha}, β={beta}, γ={gamma}')
plt.xlim(0,)
plt.ylim(0,4)
plt.legend()
plt.xlabel('t')
plt.ylabel('λ(t)')
plt.title('Failure Rate [Weibull_3parameters Dist.]')
plt.show()
p73 演習問題4.1 二項分布とポアソン分布
(処理工程)
- 母確率、サンプル数、所定故障上限を設定
- 故障確率を求める関数(二項分布、ポアソン分布)を設定
- 所定故障上限まで積算する
- 両関数で計算した積算結果の誤差を算出
import math
# 設例値
prob = 0.002
number = 1000
failure_limit = 4
# 二項分布による確率F(4)
def binal(number,failure,prob):
return math.comb(number,failure) *prob**failure *(1-prob)**(number-failure)
F_binal = 0
for failure in range(failure_limit+1):
F_binal += binal(number,failure,prob)
print(f'二項分布に従う場合の確率F({failure_limit}):{round(F_binal*100,2)}%')
# ポアソン分布による確率F(4)
myu = number *prob # 平均
F_poisson = 0
for failure in range(failure_limit+1):
F_poisson += (myu**failure)/math.factorial(failure) * math.exp(-myu)
print(f'ポアソン分布に従う場合の確率F({failure_limit}):{round(F_poisson*100,2)}%')
# 誤差
error = 1-F_poisson/F_binal
print(f'誤差:{round(error*100,2)}%')
二項分布に従う場合の確率F(4):94.75% ポアソン分布に従う場合の確率F(4):94.73% 誤差:0.02%
p73 演習問題4.2 ポアソン分布
(処理工程)
- 部分集合の故障率、個数を設定
- 混合集合の平均故障数を算出
- 平均故障数、所定故障数より、確率を算出
import math
# 設定値
lambda_a = 0.5
lambda_b = 0.3
num_a = 2
num_b = 2
failure_limit = 4
# 混合集団の平均
myu_a = lambda_a * num_a
myu_b = lambda_b * num_b
myu = myu_a + myu_b
# ポアソン分布による確率
F_poisson = 0
for failure in range(failure_limit+1):
F_poisson += (myu**failure)/math.factorial(failure) * math.exp(-myu)
print(f'故障{failure_limit}台以下となる確率:{round(F_poisson*100,2)}%')
故障4台以下となる確率:97.63%
p73 演習問題4.3 ポアソン分布
(処理工程)
- 故障率、個数、時間より、平均故障数を算出
- 平均故障数、所定故障数より、確率を算出
import math
# 設定値
lambda_value = 0.005 # 故障率[/時間]
num = 20
time = 15
failure_list = [0,1] # 故障数
# 平均故障数
myu = lambda_value * num * time
# ポアソン分布による故障確率
for failure in failure_list:
P_poisson = (myu**failure)/math.factorial(failure) * math.exp(-myu)
print(f'故障{failure}台となる確率:{round(P_poisson*100,2)}%')
故障0台となる確率:22.31% 故障1台となる確率:33.47%
p74 演習問題4.4 λ、MTTF、σ、R、t
(処理工程)
- 運用時間のデータを設定
- 故障率を算出
- 故障率より、平均故障寿命、標準偏差を算出
- 故障率と所定運用時刻より、信頼度を算出
- 故障率と所定信頼度より、運用時刻を算出
import math
Ope_hours = [380,60,140,430,230,310,100,160,270,290,190,250,210,340]
time_2 = 300 # (2)の運用時間
R_2 = 0.9 # (3)の信頼度
# (1) 故障率λ、平均故障寿命MTTF、標準偏差σ
lambda_value = len(Ope_hours)/sum(Ope_hours) # 故障率
MTTF = 1/lambda_value
sigma = 1/lambda_value
print(f'平均故障寿命MTTF:{MTTF}時間')
print(f'標準偏差σ:{sigma}時間')
# (2) 信頼度R
R_value = math.exp(-lambda_value * time_2)
print(f'運用{time}時間における信頼度R:{round(R_value*100,2)}%')
# (3) 運用時間t
t_3 = math.log(R_2)/(-lambda_value)
print(f'信頼度{R_2*100}%となる運用時間t:{round(t_3,2)}時間')
平均故障寿命MTTF:240.0時間 標準偏差σ:240.0時間 運用300時間における信頼度R:28.65% 信頼度90.0%となる運用時間t:25.29時間
p74 演習問題4.5 信頼度
(処理工程)
- 平均、分散を設定
- 正規分布の左側確率を計算
from scipy.stats import norm
import math
# 平均
myu_a = 65
myu_b = 70
# 分散
var_a = 25
var_b = 100
# 設定時刻
time = 50
# 確率
prob_a = norm.cdf((myu_a-time)/math.sqrt(var_a))
prob_b = norm.cdf((myu_b-time)/math.sqrt(var_b))
print(f'時刻{time}時間における信頼度R_A:{round(prob_a*100,4)}%')
print(f'時刻{time}時間における信頼度R_B:{round(prob_b*100,4)}%')
時刻50時間における信頼度R_A:99.865% 時刻50時間における信頼度R_B:97.725%
p74 演習問題4.6(1) 和の平均、分散
(処理工程)
- 所定の各時間の平均、分散を設定
- 各時間の和について、平均、分散を計算
- 分散より標準偏差を計算
- 一覧表示
import pandas as pd
import math
from scipy.stats import norm
# 設定値のDF化
ind_list = ['故障検知時間','修理時間','再調整時間']
col_list = ['平均','分散']
DF = pd.DataFrame([[6,5],[20,7],[3,4]],index=ind_list, columns=col_list)
DF.loc['総修復時間'] = DF.sum()
# 和の平均、分散
MTTR = DF['平均']['総修復時間']
sigma = math.sqrt(DF['分散']['総修復時間'])
print(f'総修復時間の期待値MTTR:{MTTR}分')
print(f'総修復時間の標準偏差σ:{sigma}分')
DF
総修復時間の期待値MTTR:29分 総修復時間の標準偏差σ:4.0分 平均 分散 故障検知時間 6 5 修理時間 20 7 再調整時間 3 4 総修復時間 29 16
p74 演習問題4.6(2) 所定時間以上となる確率=左側確率
(処理工程)
- 10台の総修復時間の平均、分散を計算
- 総修復時間5時間に対応する左側確率を求める
# コードは上記の続き
time = 5 *60
DF.loc['10台の総修復時間'] = DF.loc['総修復時間']*10
myu10 = DF['平均']['10台の総修復時間']
var10 = DF['分散']['10台の総修復時間']
# 左側確率
prob = norm.cdf((myu10-time)/math.sqrt(var10))
print(f'総修復時間が{time}分以上となる確率P:{round(prob*100,2)}%')
DF
総修復時間が300分以上となる確率P:21.46% 平均 分散 故障検知時間 6 5 修理時間 20 7 再調整時間 3 4 総修復時間 29 16 10台の総修復時間 290 160
p74 演習問題4.7
(処理工程)
- α、β、γパラメータを設定
- 公式(平均、標準偏差、信頼度、故障率)に代入
from scipy.special import gamma
import math
# 設定値
alpha, beta, gam = 4,80,15
time = 100 # (2)の設定時間
# 平均μ
myu = gam + beta * gamma(1+1/alpha)
print(f'平均故障寿命MTTF:{round(myu,2)}時間')
# 標準偏差σ
std = beta * (math.sqrt(gamma(1+2/alpha)-(gamma(1+1/alpha))**2))
print(f'標準偏差σ:{round(std,2)}時間')
# 信頼度R
Rel = math.exp(-((time-gam)/beta)**alpha)
print(f'時刻{time}時間における信頼度R:{round(Rel*100,2)}%')
# 故障率λ
lam = alpha/beta * ((time-gam)/beta)**(alpha-1)
print(f'時刻{time}時間における故障率λ:{round(lam*100,3)}%')
平均故障寿命MTTF:87.51時間 標準偏差σ:20.34時間 時刻100時間における信頼度R:27.96% 時刻100時間における故障率λ:5.997%