「信頼性工学のはなし―信頼度99.9999…%をめざして」7章
大村平「信頼性工学のはなし―信頼度99.9999…%をめざして」日科技連 の読後行間補充メモ
同書籍は、印刷数表による信頼性工学の啓蒙書。
本稿では、同書籍の設例について、Python ［Google Colaboratory］による演算処理例を示す。
７章 データで信頼性を判断する
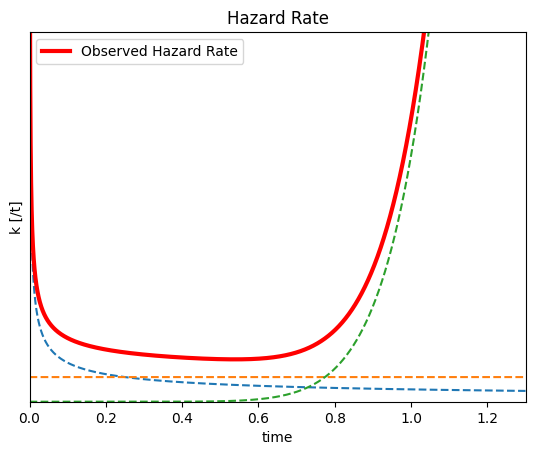
p149 図7.1上図 ３種類の分布 故障率kのグラフ
ワイブル故障分布（p151）
\begin{eqnarray*} f(t)&=&k(t)\times R(t)\\&=&\cfrac{m}{\eta}\left(\cfrac{t-\gamma}{\eta}\right)^{m-1} \times e^{-\left( \cfrac{t-\gamma}{\eta}\right)^m}\end{eqnarray*}
を構成する故障率関数
\(k(t)=\cfrac{m}{\eta} \left(\cfrac{t-\gamma}{\eta}\right)^{m-1}\)
を使用する。
式中の各パラメータの趣旨は、以下のとおり。
- \(m\) …形状パラメータ
- \(\eta\) …尺度パラメータ
- \(\gamma\) …位置パラメータ
（期間による\(m\) の値）
- 初期故障期間 \(m<1\)
- 偶発故障期間 \(m=1\)
- 摩耗故障期間 \(m>1\)
# 故障確率k
import numpy as np
import math
from matplotlib import pyplot as plt
# 設定値
m_list = [0.5, 1, 10] # 形状パラメータ（初期、偶発、摩耗）
eta_value = 1 # 尺度パラメータ(半減期、時定数)
gamma_value = 0 # 位置パラメータ
# 各時期（初期、偶発、摩耗）のパラメータ設定
g_wide =1.3 # グラフ横幅
step = 0.0001 # グラフ描画刻み
p1 = [0, g_wide, m_list[0], eta_value, gamma_value] # 始点、終点、形状、尺度、位置
p2 = [0, g_wide, m_list[1], eta_value, gamma_value]
p3 = [0, g_wide, m_list[2], eta_value, gamma_value]
graph_list = [p1,p2,p3] # リスト化
# 関数 故障確率 k (ワイブル)
def k_weibull(m_value,eta_value,gamma_value,time): # 形状、尺度、位置、時間
khead = m_value/eta_value
ktail = (time - gamma_value)/eta_value
kpower = m_value -1
y_value = khead * ktail ** kpower
return y_value
# 関数 グラフ用データ
def xylist(function,start,end,m_value,eta_value,gamma_value): # 関数、始点、終点、形状、尺度、位置
x_list = []
y_list = []
for time in np.arange(start,end,step):
x_list.append(time) # 時間リスト
y_list.append(function(m_value,eta_value,gamma_value,time)) # 演算結果リスト
return x_list, y_list
# 各グラフのパラメータを関数（グラフ用データ）に渡して、描画
ky_lists = []
for graph in graph_list:
x_data = xylist(k_weibull, graph[0],graph[1],graph[2],graph[3],graph[4])[0]
y_data = xylist(k_weibull, graph[0],graph[1],graph[2],graph[3],graph[4])[1]
plt.plot(x_data, y_data, linestyle="--")
ky_lists.append(y_data)
# バスタブ曲線
ky_lists[2] = np.nan_to_num(ky_lists[2], nan=0) # nan を0に置換
ky_sums = [x+y+z for (x,y,z) in zip(ky_lists[0], ky_lists[1],ky_lists[2])] # ３データを合計
plt.plot(x_data, ky_sums, label="Observed Hazard Rate", color='red', linewidth=3)
# グラフ凡例等
plt.xlim(0,g_wide)
plt.ylim(0,15)
plt.yticks([])
plt.xlabel('time')
plt.ylabel('k [/t]')
plt.legend()
plt.title('Hazard Rate')
plt.show()
- 初期故障期間の故障率が高く、時間経過とともに急減する。
- 偶発故障期間は低め安定となる。
- 摩耗故障期間は、故障率が増加傾向に転じる。
p149 信頼度R のグラフ
ワイブル故障分布（p151）
\begin{eqnarray*} f(t)&=&k(t)\times R(t)\\&=&\cfrac{m}{\eta}\left(\cfrac{t-\gamma}{\eta}\right)^{m-1} \times e^{-\left( \cfrac{t-\gamma}{\eta}\right)^m}\end{eqnarray*}
を構成する信頼度関数
\(R(t)= e^{-\left( \cfrac{t-\gamma}{\eta}\right)^m}\)
を使用する。
# コードは上記の続き
# 関数 信頼度Ｒ (ワイブル)
def R_weibull(m_value,eta_value,gamma_value,time): # 形状、尺度、位置、時間
r_core = ((time - gamma_value)/eta_value) ** m_value
y_value = math.exp(-r_core)
return y_value
# 各グラフのパラメータを関数（グラフ用データ）に渡して、描画
R_ylist = []
for graph in graph_list:
x_data = xylist(R_weibull,graph[0],graph[1],graph[2],graph[3],graph[4])[0]
y_data = xylist(R_weibull,graph[0],graph[1],graph[2],graph[3],graph[4])[1]
plt.plot(x_data, y_data, linestyle="--")
R_ylist.append(y_data)
# 観測Ｒ曲線
R_ylist[2] = np.nan_to_num(R_ylist[2], nan=0) # nan を0に置換
Ry_sums = [x+y+z for (x,y,z) in zip(R_ylist[0], R_ylist[1],R_ylist[2])] # ３データを合計
plt.plot(x_data, Ry_sums, label="Observed Degree of Reliability", color='red', linewidth=2)
# グラフ凡例等
plt.xlim(0,)
plt.ylim(0,)
plt.yticks([])
plt.xlabel('time')
plt.ylabel('R [%]')
plt.legend()
plt.title('Degree of Reliability')
plt.show()
- 初期故障期間に信頼度が強く下がる。
- 偶発故障期間は漸減傾向にある。
- 摩耗故障期間に入ると減少傾向が強まる。
p149 図7.1下図 ＝p157 図7.6上図 ３種類の分布 故障分布f のグラフ
ワイブル故障分布の関数（p151）
\begin{eqnarray*} f(t)&=&k(t)\times R(t)\\&=&\cfrac{m}{\eta}\left(\cfrac{t-\gamma}{\eta}\right)^{m-1} \times e^{-\left( \cfrac{t-\gamma}{\eta}\right)^m}\end{eqnarray*}
を使用する。
# コードは上記の続き
# 関数 信頼度 f (ワイブル)
def F_weibull(m_value,eta_value,gamma_value,time): # 形状、尺度、位置、時間
R_value = math.exp(-(((time - gamma_value)/eta_value) ** m_value))
k_value = (m_value/eta_value) * ((time - gamma_value)/eta_value) ** (m_value -1)
return R_value * k_value
# 各グラフのパラメータを関数（グラフ用データ）に渡して、描画
f_ylists = []
for graph in graph_list:
x_data = xylist(F_weibull, graph[0],graph[1],graph[2],graph[3],graph[4])[0]
y_data = xylist(F_weibull, graph[0],graph[1],graph[2],graph[3],graph[4])[1]
plt.plot(x_data, y_data, linestyle="--")
f_ylists.append(y_data)
# 観測ｆ曲線
f_ylists[2] = np.nan_to_num(f_ylists[2], nan=0) # nan を0に置換
fy_sums = [x+y+z for (x,y,z) in zip(f_ylists[0], f_ylists[1],f_ylists[2])] # ３データを合計
plt.plot(x_data, fy_sums, label="Observed failure rate", color='red', linewidth=2)
# グラフ凡例等
plt.xlim(0,)
plt.ylim(0,5)
plt.yticks([])
plt.xlabel('time')
plt.ylabel('f [%/t]')
plt.legend()
plt.title('f probability distribution')
plt.show()
- 初期故障期間の故障率は高い。
- 偶発故障期間の故障率は低めで安定する。
- 摩耗故障期間の故障率が一時増加するが、残数減に伴い収束する。
p149 ＝p157 図7.6下図 故障割合F のグラフ
- 信頼度\(R\) の補数として計算。
- 故障分布\(f\) を積分することでも、同じ値が得られる。
# コードは上記の続き
# 観測Ｆ曲線
Fy_sums = [Ry_sums[0]-Ry for Ry in Ry_sums] # Rの補数
plt.plot(x_data, Fy_sums, label="Cumulative Failure rate", color='red', linewidth=2)
# グラフ凡例等
plt.xlim(0,)
plt.ylim(0,)
plt.yticks([])
plt.xlabel('time')
plt.ylabel('F [%]')
plt.legend()
plt.title('Failure rate')
plt.show()
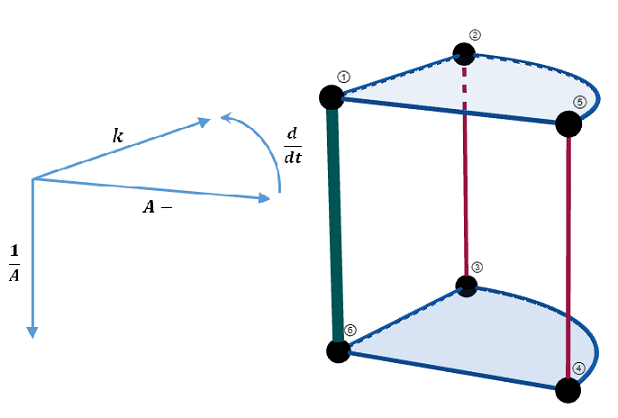
p149とp157 の各グラフの位置づけ（＝p71 グラフ ① ～ ⑥ の相互関係）
- ① 残存数\(y\)
- ② 新規故障数\(\Delta y\)
- ③ 新規故障の対全体割合（故障の分布）\(f\)
- ④ 故障数の対全体割合\(F\)
- ⑤ 故障数の累計\(\sum \Delta y\)
- ⑥ 残存割合（信頼度）\(R\)
- 新規故障の対残存割合（故障率）\(k\)
残存系①⑥ vs 故障系②③④⑤
- 総数 \(Ａ\) で除する： ①②⑤平面［個数］ \(\Longrightarrow\) ⑥③④平面［割合］
- 故障率 \(k\) を乗ずる： ①⑥軸 \(\Longrightarrow\) ②③軸［瞬間故障］
- 補数をとる： ①⑥軸 \(\Longrightarrow\) ⑤④軸［故障累計］
- 微分する： ⑤④軸 \(\Longrightarrow\) ②③軸
p152 図7.3 ワイブル分布の例
# 図7.3
import numpy as np
import math
import matplotlib.pyplot as plt
# 関数（Weibull distribution）
def Weibull(m,eta,gamma,time):
return ((m*(time-gamma)**(m-1))/eta**m) * (math.e)**(-((time-gamma)/eta)**m)
# 関数（時間と故障率）
def Weibul_Data(eta,m,gamma):
time = [] #時間
fr = [] #故障率
for t in np.arange(0,4,0.01):
time.append(t)
WE = Weibull(m,eta,gamma,t)
fr.append(WE)
return time,fr
# パラメータ
m_value = 2 #形状
eta = 1 #尺度（指数分布のMTBFに相当）
gamma = 1 #位置（無故障の期間）
# グラフの描画
time_data = Weibul_Data(eta,m_value,gamma)[0]
fr_data = Weibul_Data(eta,m_value,gamma)[1]
plt.plot(time_data, fr_data,label= f'm={m_value}\neta={eta}\ngamma={gamma}')
plt.xlabel('time')
plt.ylabel('failure rate')
plt.xlim(0,4)
plt.ylim(0,)
plt.yticks([])
plt.legend()
plt.title(f'Weibul')
p153 図7.4 ワイブル分布の例（形状パラメータ m による違い）
# 図7.3
import numpy as np
import math
import matplotlib.pyplot as plt
# 関数（Weibull distribution）
def Weibull(m,eta,gamma,time):
return ((m*(time-gamma)**(m-1))/eta**m) * (math.e)**(-((time-gamma)/eta)**m)
# 関数（時間と故障率）
def Weibul_Data(eta,m,gamma):
time = [] #時間
fr = [] #故障率
for t in np.arange(0,4,0.01):
time.append(t)
WE = Weibull(m,eta,gamma,t)
fr.append(WE)
return time,fr
# パラメータ
m_value = 2 #形状
eta = 1 #尺度（指数分布のMTBFに相当）
gamma = 1 #位置（無故障の期間）
# グラフの描画
time_data = Weibul_Data(eta,m_value,gamma)[0]
fr_data = Weibul_Data(eta,m_value,gamma)[1]
plt.plot(time_data, fr_data,label= f'm={m_value}\neta={eta}\ngamma={gamma}')
plt.xlabel('time')
plt.ylabel('failure rate')
plt.xlim(0,4)
plt.ylim(0,)
plt.yticks([])
plt.legend()
plt.title(f'Weibul')
p160 故障時刻 t と故障割合 F(t)
import pandas as pd t_value = [1, 3, 7, 18] # 故障時刻（横下軸） denominator = len(t_value)+1 #要素数 F_value = [] # 累積故障割合（縦左軸） for item in range(1,denominator): # 要素数繰り返す F_value.append(item/denominator) DF = pd.DataFrame([t_value,F_value]).T DF.columns =['Time','F(t)'] DF
Time F(t) 0 1.0 0.2 1 3.0 0.4 2 7.0 0.6 3 18.0 0.8
p160 図7.7 =p166 図7.10 mと η を求める実例 その１
検査対象が、初期故障・偶発故障・摩耗故障期間のいずれの状態にあるかを判定するため、\(m\) を算出する。
（作業工程）
- ワイブル確率紙の画面を設定する（対数表示によるデータの直線化判定のため）
- 観測値をプロットし、近似直線を描画（直線判定→ワイブル分布と認定）
- 形状パラメータ\(m\) を\(y\)軸切片の負数として取得
- 尺度パラメータ\(\eta\) を\(x\) 軸切片として取得
from matplotlib import pyplot as plt
import matplotlib as mpl
import numpy as np
fig = plt.figure()
ax1 = fig.subplots()
ax2 = ax1.twiny()
ax3 = ax2.twinx()
# 観測値のプロット（X軸Y軸の平面へ）
ax3.scatter(X_value, Y_value, c="red", s =60 ,label="X_Y")
ax3.scatter(1, 0, c="blue", s=60, label="Estimated point of m")
# 近似直線
a_value, b_value = np.polyfit(X_value, Y_value, 1)
X2_value = np.linspace(-2,4)
Y2_value = [a_value * Xs +b_value for Xs in X2_value]
ax3.plot(X2_value, Y2_value, linestyle = '--', color = 'red')
# 座標(1,0)の点ｍ を通る直線 (y-0)=a(x-1)
Y3_value = [a_value * Xs -a_value for Xs in X2_value]
ax3.plot(X2_value, Y3_value, linestyle = '--', color = 'blue')
# 上記直線のｙ切片
y_intercept = a_value * 0 -a_value # 直線式に x=0 を代入した値
print(f'傾きｍ＝ －（切片値）：{-round(y_intercept,2)}')
# 近似直線のｘ切片
x_intercept = -b_value/a_value # 近似式に y=0 を代入した値
tx_intercept = math.exp(x_intercept) # ｔ値に換算
print(f'尺度η＝：{round(tx_intercept,2)}')
# ｔ軸、Ｆ軸のスケール
ax1.set_xscale('log')
ax1.yaxis.set_ticks([])
# X軸、Y軸のスケール
ax3.set_xscale('linear')
ax3.set_yscale('linear')
# 目盛り
ax1.set_xlim(0.1, 100)
ax3.set_xlim(-2, 4)
ax3.set_ylim(-7, 2)
# 軸名
ax1.set_xlabel('t [ln]')
ax1.set_ylabel('F [lnln]')
ax2.set_xlabel(r'$X=ln(t)$')
ax3.set_ylabel(r'$Y=lnln\left(\frac{1}{1-F}\right)$')
# X軸、Y軸
ax2.axvline(x=0, color='black')
ax3.axhline(y=0, color='black')
# 補助線
ax1.grid()
ax2.grid()
ax3.grid()
# 凡例
h1, l1 = ax1.get_legend_handles_labels()
h3, l3 = ax3.get_legend_handles_labels()
ax1.legend(h1 + h3, l1 + l3, loc='right')
plt.show()
傾きｍ＝ －（切片値）：0.69 尺度η＝：8.45
p162 図7.8 mを求める実例（その２）
import pandas as pd
import numpy as np
import math
from matplotlib import pyplot as plt
import matplotlib as mpl
t_value = [5, 7, 9, 11, 14] # 故障経過日（横下軸）
denominator = len(t_value)+1 #要素数
F_value = [] # 累積故障割合（縦左軸）
for item in range(1,denominator): # 要素数繰り返す
F_value.append(item/denominator)
F_per = [round(Fs*100,1) for Fs in F_value]
DF = pd.DataFrame([t_value, F_per]).T
DF.columns =['Time [Days]','F(t) [%]']
display(DF)
X_value = [round(math.log(t),2) for t in t_value] # 横上軸
Y_value = [round(math.log(math.log(1/(1-F))),2) for F in F_value] # 縦右軸
# グラフ
fig = plt.figure()
ax1 = fig.subplots()
ax2 = ax1.twiny()
ax3 = ax2.twinx()
# 観測値のプロット（X軸Y軸の平面へ）
ax3.scatter(X_value, Y_value, c="red", s =60 ,label="X_Y")
ax3.scatter(1, 0, c="blue", s=60, label="Estimated point of m")
# 近似直線
a_value, b_value = np.polyfit(X_value, Y_value, 1)
X2_value = np.linspace(-2,4)
Y2_value = [a_value * Xs +b_value for Xs in X2_value]
ax3.plot(X2_value, Y2_value, linestyle = '--', color = 'red')
# 座標(1,0)の点ｍ を通る直線 (y-0)=a(x-1)
Y3_value = [a_value * Xs -a_value for Xs in X2_value]
ax3.plot(X2_value, Y3_value, linestyle = '--', color = 'blue')
# 上記直線のｙ切片
intercept = a_value * 0 -a_value # 直線式に x=0 を代入した値
print(f'傾きｍ＝ －（切片値）：{-round(intercept,2)}')
# ｔ軸、Ｆ軸のスケール
ax1.set_xscale('log')
ax1.yaxis.set_ticks([])
# X軸、Y軸のスケール
ax3.set_xscale('linear')
ax3.set_yscale('linear')
# 目盛り
ax1.set_xlim(0.1, 100)
ax3.set_xlim(-2, 4)
ax3.set_ylim(-7, 2)
# 軸名
ax1.set_xlabel('t [ln]')
ax1.set_ylabel('F [lnln]')
ax2.set_xlabel(r'$X=ln(t)$')
ax3.set_ylabel(r'$Y=lnln\left(\frac{1}{1-F}\right)$')
# X軸、Y軸
ax2.axvline(x=0, color='black')
ax3.axhline(y=0, color='black')
# 補助線
ax1.grid()
ax2.grid()
ax3.grid()
# 凡例
h1, l1 = ax1.get_legend_handles_labels()
h3, l3 = ax3.get_legend_handles_labels()
ax1.legend(h1 + h3, l1 + l3, loc='right')
plt.show()
Time [Days] F(t) [%] 0 5.0 16.7 1 7.0 33.3 2 9.0 50.0 3 11.0 66.7 4 14.0 83.3 傾きｍ＝ －（切片値）：2.22
p163 表7.1 データが直線に並ばない場合（γ 補正）
観測値をプロットした結果、ただちに近似直線を描画できない場合でも、\(\gamma\) 値が０以外である可能性を探索する。適切な\(\gamma\) 値を全データから減算することで、直線判定できる場合、ワイブル分布と認定する。
（作業工程）
- ワイブル確率紙の画面を設定する
- 観測値をプロットし、近似曲線を描画
- 近似曲線と確率紙底辺との交点を、\(\gamma\) 値候補として抽出
- 同\(\gamma\) 候補値ないしは近似する候補値を、全データから減算する（対数表示画面上の移動距離はデータにより異なる）
- 修正後データを再プロットし、近似直線を描画（直線判定→ワイブル分布と認定）
- 形状パラメータ\(m\) を\(y\) 軸切片の負数として取得
import pandas as pd
import numpy as np
import math
from matplotlib import pyplot as plt
import matplotlib as mpl
from scipy.optimize import curve_fit
t_value = [7, 9, 11, 13, 15, 18, 21, 27, 35] # 故障までの経過回数（横下軸）
denominator = len(t_value)+1 #要素数
F_value = [] # 累積故障割合（縦左軸）
for item in range(1,denominator): # 要素数繰り返す
F_value.append(item/denominator)
F_per = [round(Fs*100,1) for Fs in F_value]
DF = pd.DataFrame([t_value, F_per]).T
DF.columns =['Time [回]','F(t) [%]']
display(DF)
X_value = [math.log(t) for t in t_value] # 横上軸
Y_value = [math.log(math.log(1/(1-F))) for F in F_value] # 縦右軸
# グラフ
fig = plt.figure()
ax1 = fig.subplots()
ax2 = ax1.twiny()
ax3 = ax2.twinx()
# 観測値のプロット（X軸Y軸の平面へ）
ax3.scatter(X_value, Y_value, c="red", s =60 ,label="X_Y")
ax3.scatter(1, 0, c="blue", s=60, label="Estimated point of m")
# 近似直線
a_value, b_value = np.polyfit(X_value, Y_value, 1)
X2_value = np.linspace(-2,4)
Y2_value = [a_value * Xs +b_value for Xs in X2_value]
ax3.plot(X2_value, Y2_value, linestyle = '--', color = 'red')
# 座標(1,0)の点ｍ を通る直線 (y-0)=a(x-1)
Y3_value = [a_value * Xs -a_value for Xs in X2_value]
ax3.plot(X2_value, Y3_value, linestyle = '--', color = 'blue')
# 上記直線のｙ切片
intercept = a_value * 0 -a_value # 直線式に x=0 を代入した値
print(f'傾きｍ＝ －（切片値）：{-round(intercept,2)}')
# 近時曲線
def func(x, a, b):
return a + b * np.log(x) # モデル関数
a_pred, b_pred = curve_fit(func, X_value, Y_value)[0] # 近似演算
# 近似曲線の描画
X3_value = np.linspace(0.1,4)
y_pred = func(X3_value, a_pred, b_pred)
ax3.plot(X3_value, y_pred, "orange", linestyle = '--', label=fr"$Y={a_pred:.1f} + {b_pred:.1f} \log X$")
# 上記曲線の y=-7 切片
intercept_x = math.exp ((-7-a_pred)/b_pred) # 曲線式に y=-7 を代入したX値
intercept_t = math.exp(intercept_x) # t値へ変換
print(f'修正値候補：{int(intercept_t)}')
# ｔ軸、Ｆ軸のスケール
ax1.set_xscale('log')
ax1.yaxis.set_ticks([])
# X軸、Y軸のスケール
ax3.set_xscale('linear')
ax3.set_yscale('linear')
# 目盛り
ax1.set_xlim(0.1, 100)
ax3.set_xlim(-2, 4)
ax3.set_ylim(-7, 2)
# 軸名
ax1.set_xlabel('t [ln]')
ax1.set_ylabel('F [lnln]')
ax2.set_xlabel(r'$X=ln(t)$')
ax3.set_ylabel(r'$Y=lnln\left(\frac{1}{1-F}\right)$')
# X軸、Y軸
ax2.axvline(x=0, color='black')
ax3.axhline(y=0, color='black')
# 補助線
ax1.grid()
ax2.grid()
ax3.grid()
# 凡例
h1, l1 = ax1.get_legend_handles_labels()
h3, l3 = ax3.get_legend_handles_labels()
ax1.legend(h1 + h3, l1 + l3, loc='lower right')
plt.show()
Time [回] F(t) [%] 0 7.0 10.0 1 9.0 20.0 2 11.0 30.0 3 13.0 40.0 4 15.0 50.0 5 18.0 60.0 6 21.0 70.0 7 27.0 80.0 8 35.0 90.0 傾きｍ＝ －（切片値）：1.87 修正値候補：2
p164 表7.2 修正した t~F(t) と直線判定
修正候補（\(\gamma=2\)）では、なお曲線をとどめていたので、\(\gamma=5\) を採用した。
# コードは上記の続き
t_value_fix = [ts - 5 for ts in t_value] # 修正値5 とすると直線になる
denominator = len(t_value_fix)+1 #要素数
F_value = [] # 累積故障割合（縦左軸）
for item in range(1,denominator): # 要素数繰り返す
F_value.append(item/denominator)
F_per = [round(Fs*100,1) for Fs in F_value]
DF = pd.DataFrame([t_value_fix, F_per]).T
DF.columns =['Time [回]','F(t) [%]']
display(DF)
XNvalue = [round(math.log(t),2) for t in t_value_fix] # 横上軸
Y_value = [round(math.log(math.log(1/(1-F))),2) for F in F_value] # 縦右軸
# グラフ
fig = plt.figure()
ax1 = fig.subplots()
ax2 = ax1.twiny()
ax3 = ax2.twinx()
# 観測値のプロット（X軸Y軸の平面へ）
ax3.scatter(X_value, Y_value, c="red", s =60 ,label="X_Y(original)")
ax3.scatter(XNvalue, Y_value, c="green", s =60 ,label="X_Y(revised)")
ax3.scatter(1, 0, c="blue", s=60, label="Estimated point of m")
# 近似曲線
ax3.plot(X3_value, y_pred, "orange", linestyle = '--', label=fr"$Y={a_pred:.1f} + {b_pred:.1f} \log X$")
# 近似直線
a_value, b_value = np.polyfit(XNvalue, Y_value, 1)
X2_value = np.linspace(-2,4)
Y2_value = [a_value * Xs +b_value for Xs in X2_value]
ax3.plot(X2_value, Y2_value, linestyle = '--', color = 'green')
# 座標(1,0)の点ｍ を通る直線 (y-0)=a(x-1)
Y3_value = [a_value * Xs -a_value for Xs in X2_value]
ax3.plot(X2_value, Y3_value, linestyle = '--', color = 'blue')
# 上記直線のｙ切片
intercept = a_value * 0 -a_value # 直線式に x=0 を代入した値
print(f'傾きｍ＝ －（切片値）：{-round(intercept,2)}')
# ｔ軸、Ｆ軸のスケール
ax1.set_xscale('log')
ax1.yaxis.set_ticks([])
# X軸、Y軸のスケール
ax3.set_xscale('linear')
ax3.set_yscale('linear')
# 目盛り
ax1.set_xlim(0.1, 100)
ax3.set_xlim(-2, 4)
ax3.set_ylim(-7, 2)
# 軸名
ax1.set_xlabel('t [ln]')
ax1.set_ylabel('F [lnln]')
ax2.set_xlabel(r'$X=ln(t)$')
ax3.set_ylabel(r'$Y=lnln\left(\frac{1}{1-F}\right)$')
# X軸、Y軸
ax2.axvline(x=0, color='black')
ax3.axhline(y=0, color='black')
# 補助線
ax1.grid()
ax2.grid()
ax3.grid()
# 凡例
h1, l1 = ax1.get_legend_handles_labels()
h3, l3 = ax3.get_legend_handles_labels()
ax1.legend(h1 + h3, l1 + l3, loc='lower right')
plt.show()
Time [回] F(t) [%] 0 2.0 10.0 1 4.0 20.0 2 6.0 30.0 3 8.0 40.0 4 10.0 50.0 5 13.0 60.0 6 16.0 70.0 7 22.0 80.0 8 30.0 90.0 傾きｍ＝ －（切片値）：1.16
p173 検査特性曲線（OC曲線）
（作業工程）
- OC曲線のグラフ用データを生成する関数を設定（引数：標本個数、許容不良品率、演算範囲）
- 標本個数は比較のため複数設定（50個の場合、150個の場合）
- ロット不良率、許容不良率は、共通数値を設定
- OC曲線関数で演算し、グラフ化
- 生産者危険と消費者危険を計算し、表示
import math
from matplotlib import pyplot as plt
# 関数 OC曲線
def OC_curve_n (snumber,percent, xrange): # 標本個数、許容不良品率、横軸演算範囲を入力
LOT_P = [] # ロットの真の不良率（グラフ横軸データ）
Series_LPR = [] # ロットが合格する割合（グラフ縦軸データ）
permissable = int(snumber *percent/100) # 許容不良品個数
for lotp in range(0, xrange*10, 1):
prob = lotp/1000 # 0～0.2 の数値
LOT_P.append(lotp/10) # 0～20 の数値をｘ軸要素として格納
items = range(0, snumber) # 0個～標本個数
Ps = [] # 個別の事象確率
for r in items: # 標本個数の全場合について
Probability = (snumber*prob)**r/math.factorial(r)*(math.exp(-snumber*prob))
Ps.append(Probability)
Lot_Pass_Rate = 0
for pm in range(0,permissable+1): # 許容不良品個数に至るまで
Lot_Pass_Rate += Ps[pm]*100 # ロットが合格する確率を積算
Series_LPR.append(Lot_Pass_Rate)
return [LOT_P,Series_LPR] # グラフ横軸・縦軸データを戻す
# 関数を使用して演算
xrange =8 # ロット不良率８%まで計算
percent = 2 # 許容不良品率[％]
LDR, LPR_050 = OC_curve_n(50, percent, xrange)
LDR, LPR_150 = OC_curve_n(150, percent, xrange)
# 理想の判定基準
p0 = 1 # ロットを全て合格としてよいロットの真の不良品％
p1 = 5 # ロットを全て不合格としたいロットの真の不良品％
# 生産者危険α
alpha_050 = LPR_050[p0*10]
alpha_150 = LPR_150[p0*10]
# 消費者危険β
beta_050 = LPR_050[p1*10]
beta_150 = LPR_150[p1*10]
#グラフを表示
fig = plt.figure(figsize = (6,4), facecolor='lightgrey')
plt.plot(LDR, LPR_050, color='lightblue', label=f'~1 in 50')
plt.plot(LDR, LPR_150, color='pink', label=f'~3 in 150')
# 表示バッファ
buf = 0.04
# 生産者危険αを表示
plt.vlines(p0,0,alpha_050, linestyle='dotted', color='grey',linewidth=2)
plt.vlines(p0-buf,alpha_050,100, color='blue',linewidth=2, label=fr'$\alpha$')
plt.vlines(p0+buf,alpha_150,100, color='red',linewidth=2, label=fr'$\alpha’$')
plt.hlines(100,0,xrange,color='grey',linewidth=1)
print(f'生産者危険α：{round((100-alpha_050),1)}％')
print(f'生産者危険α’：{round((100-alpha_150),1)}％')
# 消費者危険βを表示
plt.vlines(p1+buf,0,beta_050, color='lightgreen',linewidth=2, label=fr'$\beta$')
plt.vlines(p1-buf,0,beta_150, color='orange',linewidth=2, label=fr'$\beta’$')
print(f'消費者危険β：{round(beta_050,1)}％')
print(f'消費者危険β’：{round(beta_150,1)}％')
plt.title(f"OC curve, Allowable Rate = {percent} %")
plt.xlim(0,xrange)
plt.ylim(0,)
plt.xlabel('Defective Product Rate in Lot [%]')
plt.ylabel('Lot Pass Rate [%]')
plt.legend(loc = 'right')
plt.show()
生産者危険α：9.0％ 生産者危険α’：6.6％ 消費者危険β：28.7％ 消費者危険β’：5.9％
p174 表7.3 JIS Z 9002
同表の \(p_0 = 0.901～1.12\)％ に記載の抜取個数 \(n\) と合格判定基準数 \(c\) に対応する生産者リスク \(\alpha\) と消費者リスク \(\beta\) を試算した結果。
import pandas as pd
import math
from decimal import Decimal
# 数表データ
p1col = pd.DataFrame([3.55,4.50,5.6,7.1,9,11.2,14]) # p1上限
p1col_under = pd.DataFrame([2.81,3.56,4.51,5.61,7.11,9.01,11.3]) # p1下限
p0901n = pd.DataFrame([300,200,120,80,60,40,30]) # 表7.3 標本数(0.901～1.12行)
p0901c = pd.DataFrame([6,4,3,2,2,1,1]) # 表7.3 許容不良品数(0.901～1.12行)
DF_p0901 = pd.concat([p1col, p1col_under, p0901n, p0901c], axis=1).T
DF_p0901.index = ['p1_upper[%]','p1_lower[%]','sumple[個]','clear[個]']
# 関数（ロット不良品率、標本数、許容不良品数）→ロット合格率、不合格率
def RiskRate(prob_per, snumber, allowed):
prob = prob_per/100 # 演算用
defective = range(0, snumber)
Probs = []
for defect in defective:
Probability = Decimal((snumber*prob)**defect)/Decimal(math.factorial(defect))*Decimal((math.e)**(-snumber*prob))
Probs.append(float(Probability))
Lot_Pass_Rate = 0
for pm in range(0,allowed+1):
Lot_Pass_Rate += Probs[pm]
return round(Lot_Pass_Rate*100,1), round(100-Lot_Pass_Rate*100,1)
# 生産者リスク上限の行を追加
supplier_risk = []
for i in DF_p0901.columns:
supplier_risk.append(RiskRate(1.12,int(DF_p0901[i][2]),int(DF_p0901[i][3]))[1])
DF_p0901.loc["α_upper[%]"] = supplier_risk
# 生産者リスク下限の行を追加
supplier_risk = []
for i in DF_p0901.columns:
supplier_risk.append(RiskRate(0.901,int(DF_p0901[i][2]),int(DF_p0901[i][3]))[1])
DF_p0901.loc["α_lower[%]"] = supplier_risk
# 消費者リスク上限の行を追加
user_risk = []
for j in DF_p0901.columns:
user_risk.append(RiskRate(DF_p0901[j][1],int(DF_p0901[j][2]),int(DF_p0901[j][3]))[0])
DF_p0901.loc["β_upper[%]"] = user_risk
# 消費者リスク下限の行を追加
user_risk = []
for j in DF_p0901.columns:
user_risk.append(RiskRate(DF_p0901[j][0],int(DF_p0901[j][2]),int(DF_p0901[j][3]))[0])
DF_p0901.loc["β_lower[%]"] = user_risk
DF_p0901
もっとも、境界領域では、同数値を超過しているものも散見される。
p174 表7.3 抜取個数 n と合否判定基準個数 c（理論値）
- \(p_0\)：合格水準のロット不良率
- \(p_1\)：不合格水準のロット不良率
- \(\alpha\)：生産者危険
- \(\beta\)：消費者危険
- \(n\)：サンプル数
- \(c\)：合格判定基準個数
とした場合、以下の連立不等式を満足する最小の自然数の組 \(n, c\) を求めればよい（福井泰好「信頼性工学（第２版）」森北出版p136～137［計数１回抜取方式］）。
手順としては、（１）両式から導出される以下の式について、左辺（判別比）≧右辺（判別式）となるような最小の自然数\(c\) を先ず求め、（２）同\(c\) を上記連立不等式の第２式に代入して、最小の自然数\(n\) を求める。
\(\cfrac{p_1}{p_0} \geqq \cfrac{\chi^2_\beta (2(c+1))}{\chi^2_{1-\alpha} (2(c+1))}\)
（作業工程）
- 設定値を入力：\(p_0, p_1, \alpha, \beta\)
- 不良率の判別比を算定：\(p_1/p_0\)
- 判別式に自然数\(c\)を逐次代入し、判別比≧判別式となる\(c\) を取得
- 得られた\(c\) から構成される自由度に対応する\(\chi\) 二乗値から、自然数 \(n\) 値を計算
import math
from scipy.stats import chi2
# 設定値
p0 = float(input('ロット合格水準の不良率_p0[％]：',))/100
p1 = float(input('ロット不合格水準の不良率_p1[％]：',))/100
alpha = float(input('生産者危険_α[％]：',))/100
beta = float(input('消費者危険_β[％]：',))/100
# 関数 c値に対応する判別式の値
def equation(c_value):
return chi2.isf(beta,2*(c_value+1))/chi2.isf(1-alpha,2*(c_value+1))
# c値 （判別式の値 ＜ 判別比率 となる count）
dratio = p1/p0 # 判別比
count = 0
while True:
answer = equation(count)
if dratio < answer:
count +=1
else:
break
# n値
number = math.ceil(chi2.isf(beta, 2*(count+1))/(2*p1))
# c値,n値の表示
print(f'サンプル数_n：{number}\n合格判定個数_c：{count}')
ロット合格水準の不良率_p0[％]：1 ロット不合格水準の不良率_p1[％]：8 生産者危険_α[％]：5 消費者危険_β[％]：10 サンプル数_n：67 合格判定個数_c：2
p175 母集団N個から取り出した標本ｎ個が良品である場合、残個が良品である確率
import math
import pandas as pd
# 設定数値
N =10 # 母集団の個数
n = 8 # 標本数
r = 0 # 標本中の不良品数
# 関数 超幾何分布（hypergeometric distribution）
def HGD(N,k,n,r):
return math.comb(k,r)*math.comb(N-k,n-r)/math.comb(N,n)
k_values = [] # 母集団の不良品個数のリスト
p_values = [] # 母集団の不良率のリスト
Prob_values = [] # 合格確率のリスト
for k in range(0,N+1): # 全てのkについて
k_values.append(k) # 母集団中の故障品数 k列を作成
p_values.append(k/N) # 母集団中の故障品比率 p列を作成
Prob_values.append(HGD(N,k,n,r)) # 確率 P列を作成
DF = pd.DataFrame([k_values,p_values,Prob_values],
index=['k_value','p_value','Probability']).T
answer = 1/DF['Probability'].sum() # ベイズの定理
print(f'母集団の不良品率が0の確率：{round(answer*100,1)}％')
DF
母集団の不良品率が0の確率：81.8％ k_value p_value Probability 0 0.0 0.0 1.000000 1 1.0 0.1 0.200000 2 2.0 0.2 0.022222 3 3.0 0.3 0.000000 4 4.0 0.4 0.000000 5 5.0 0.5 0.000000 6 6.0 0.6 0.000000 7 7.0 0.7 0.000000 8 8.0 0.8 0.000000 9 9.0 0.9 0.000000 10 10.0 1.0 0.000000
p177 表7.4 定時打切試験による合否判定表
- \(t\)：試験時間
- \(k_1\)：ロット許容故障率
- \(R_1=e^{-k_1t}\)：ロットの信頼度
- \(\beta\)：消費者危険
- \(n\)：サンプル数
- \(c\)：合格判定基準個数
とした場合、以下の不等式を満足する最小の自然数の組 \(n, c\) を求めればよい（前掲福井「信頼性工学」p138［指数分布型計数１回抜取方式］）。
\(\sum\limits ^c_{x=0}\binom{n}{x} (1-R_1)^x R_1^{n-x}\leqq\beta\)
そこで、逐次\(c\) を代入して、左辺≦右辺となる \(n\) を求める。
import math
from scipy.special import comb
import pandas as pd
conf = 0.9 # 信頼水準
beta = 1- conf # 消費者危険 式右辺
# 関数 式左辺の値
def Lequ(k1t,num,clear):
R1 = math.exp(-k1t) # 信頼度
left =0
for x in range(clear+1):
left += comb(num, x) *((1-R1)**x) *R1**(num-x)
return left
# 関数 式左側 ≦ beta となるnum を求める
def number(k1t, clear):
num = 0
while Lequ(k1t,num,clear)>beta:
num +=1
return num
# DF化
cnum_list = [0,1,2,3,4] # 合格判定個数
kt_list = [1, 0.5, 0.2, 0.1, 0.05, 0.02, 0.01] # 許容故障率×試験時間
DF = pd.DataFrame(index =cnum_list)
for kt in kt_list:
sn_list = []
for cnum in cnum_list:
sn_list.append(number(kt, cnum))
sn_df = pd.DataFrame([sn_list]).T
DF = pd.concat([DF,sn_df],axis=1)
DF.columns = kt_list
DF
