The world inside a pillow

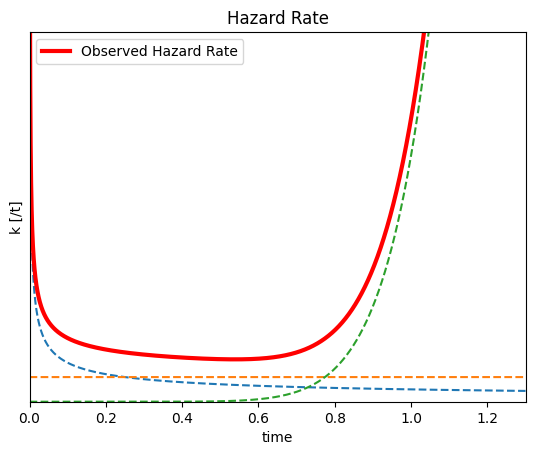
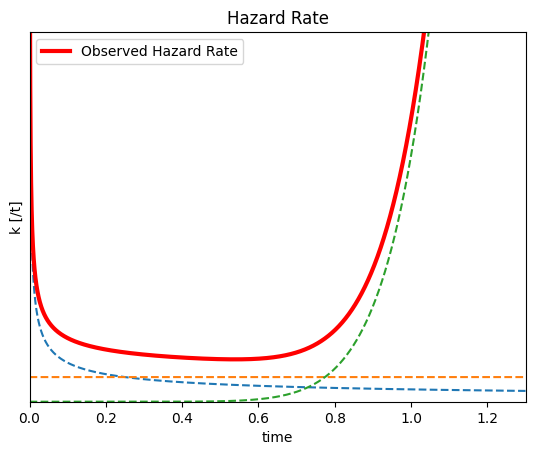
福井泰好「入門　信頼性工学（第２版）」森北出版 　の読後メモ。 設例について、Python ［Google Colaboratory］による演算処理例を示す。 3章　信頼性工学の概要 p47　図3.6　故障率λ （処理手順） ワイブル式より、DFR・CFR・IFRの各分布を計算 上記分布を合算（観測される故障率λの分布） （コード）      故障率kのグラフ 　と同じ 赤色実線：観測される故障率λ曲線（バスタブ曲線） 青色点線：DFR分布 橙色点線：CFR分布 赤色点線：IFR分布 p47　図3.6　確率密度ｆ （処理手順） ワイブル式より、DFR・CFR・IFRの各分布を計算 上記分布を合算（観測される確率密度ｆの分布） （コード）      確率密度ｆのグラフ 　と同じ 赤色実線：観測される確率密度ｆ曲線 青色点線：DFR分布 橙色点線：CFR分布 赤色点線：IFR分布 p47　図3.6　信頼度Ｒ （処理手順） ワイブル式より、DFR・CFR・IFRの各分布を計算 上記分布を合算（観測される信頼度Ｒの分布） （コード）      信頼度Rのグラフ 　と同じ 赤色実線：観測される信頼度Ｒ曲線 青色点線：DFR分布 橙色点線：CFR分布 赤色点線：IFR分布 p52　例題3.1(1)　総試験時間　定数打切り方式 （処理手順） 寿命試験結果のデータを設定 同データを、指定個数分（故障が発現済み）／未発現に区分 故障が発現済み：寿命時間を加算 故障が未発現：指定個数の最長寿命　×　未発現データ個数 各区分の計算結果を合算 time_list = [45,53,55,61,65,67,70,71,74,75] # 寿命試験結果 f_num = 4 # 故障数 t_list = sorted(time_list) # 昇順に並び替え # 故障が発現済み confirmed = t_list[:f_num] con_sum = sum(confirmed) # 故障が未発現 residual = len(t_list)-len(confirmed) res_sum = confirmed[-1] * residual # 総試験時間Tc total = con_sum + res_sum print(f'定数打切り方式（故障数{f_num}個）での総試験時

福井泰好「入門　信頼性工学（第２版）」森北出版 　の読後メモ。 設例について、Python ［Google Colaboratory］による演算処理例を示す。 １章　信頼性工学の概要 p5　図1.4　部品数と部品の信頼度Rがアイテムの信頼度におよぼす影響 （作業手順） 部品数を 1～\(10^6\) 個まで設定（グラフ横軸） 部品の信頼度\(R\)を複数設定 アイテム（直列システム全体）の信頼度を計算（グラフ縦軸） グラフ化 import numpy as np import matplotlib.pyplot as plt start = 0 end = 10**6 X_list = np.arange(start, end, 1) #部品数 R_list = [0.9, 0.99, 0.999, 0.9999, 0.99999] # 部品の信頼度 fig = plt.figure() ax = fig.add_subplot(1, 1, 1) ax.grid(color='gray') for rel in range(len(R_list)): Y_list = R_list[rel]**X_list # システム全体の信頼度 ax.plot(X_list, Y_list, label=fr'R={R_list[rel]}') plt.xscale('log') #横軸を対数目盛り plt.xlabel('Number of parts') plt.ylabel('Overall system reliability') plt.xlim(1,) # 部品点数は１以上 plt.ylim(0,) plt.legend() plt.show() 部品点数が増加するにつれて、直列システムの信頼度は減少する。 同減少度合いは、部品の信頼度が小さいほど、強い。 p11　例題1.1　信頼度R （作業手順） 故障時刻と信頼度を求めたい時刻（運用時刻）のリストを設定 特定の運用時刻における残存数を計算する関数を設定 各残存数から各信頼度を計算 一覧表化 import pandas as pd Num = 3 # アイテム数 f_time = [6,12,2

大村平「信頼性工学のはなし―信頼度99.9999…%をめざして」日科技連 　の読後行間補充メモ 同書籍は、印刷数表による信頼性工学の啓蒙書。 本稿では、同書籍の設例について、Python ［Google Colaboratory］による演算処理例を示す。 ８章　信頼性を評価する p193　Fault tree analysis OR計算を、以下の式により計算した場合の結果 \(P= 1-(1-p_1)(1-p_2)\) （作業工程） 故障木の AND/OR 関係を設定する 末端葉の故障率を設定する AND関数、OR関数で樹木全体の故障率を計算する def f_or(perlist): # OR計算 value = 1 for per in range(len(perlist)): value *= 1-perlist[per]/100 return (1-value)*100 def f_or2(perlist): # OR計算（近似値） value = 0 for per in range(len(perlist)): value += perlist[per]/100 return value*100 def f_and(perlist): # AND計算 value = 1 for per in range(len(perlist)): value *= perlist[per]/100 return value*100 # ツリー情報 a = f_or([0.1, 0.2]) b = f_or([0.1, 0.2]) c = f_and([1.0,1.0]) d = f_or([a,b]) e = f_or([0.5, 1.0]) f = f_or([c,d,e]) # 演算結果の表示 print(round(f,2),'%') 2.09 % p194　近似値計算の場合 OR計算を、以下の近似式により計算した場合の結果 \(P\fallingdotseq p_1+p2\) # コードは上記の続き # ツリー情報 a = f_or2([0.1, 0.2]) b = f_or2([0.1, 0.2]) c = f_and([1.0,1.0]) d = f_

大村平「信頼性工学のはなし―信頼度99.9999…%をめざして」日科技連 　の読後行間補充メモ 同書籍は、印刷数表による信頼性工学の啓蒙書。 本稿では、同書籍の設例について、Python ［Google Colaboratory］による演算処理例を示す。 ７章　データで信頼性を判断する p149　図7.1上図　３種類の分布　故障率kのグラフ ワイブル故障分布（p151） \begin{eqnarray*} f(t)&=&k(t)\times R(t)\\&=&\cfrac{m}{\eta}\left(\cfrac{t-\gamma}{\eta}\right)^{m-1} \times e^{-\left( \cfrac{t-\gamma}{\eta}\right)^m}\end{eqnarray*} を構成する故障率関数 \(k(t)=\cfrac{m}{\eta} \left(\cfrac{t-\gamma}{\eta}\right)^{m-1}\) を使用する。 式中の各パラメータの趣旨は、以下のとおり。 \(m\) …形状パラメータ \(\eta\) …尺度パラメータ \(\gamma\) …位置パラメータ （期間による\(m\) の値） 初期故障期間 \(m<1\) 偶発故障期間 \(m=1\) 摩耗故障期間 \(m>1\) # 故障確率k import numpy as np import math from matplotlib import pyplot as plt # 設定値 m_list = [0.5, 1, 10] # 形状パラメータ（初期、偶発、摩耗） eta_value = 1 # 尺度パラメータ(半減期、時定数) gamma_value = 0 # 位置パラメータ # 各時期（初期、偶発、摩耗）のパラメータ設定 g_wide =1.3 # グラフ横幅 step = 0.0001 # グラフ描画刻み p1 = [0, g_wide, m_list[0], eta_value, gamma_value] # 始点、終点、形状、尺度、位置 p2 = [0, g_wide, m_list[1], eta_value, gamma_value] p3 = [0, g_wide, m_list[