数学検定問題集1級
日本数学検定協会「数学検定問題集1級」創育(2018.2.1 第1版3刷)
https://www.amazon.co.jp/dp/4882299402/
例えば、多項式 \(P(x)=x^2+3x+1\) を、\((x-2)\) で割った場合の剰余 \(r\) は、剰余定理によれば、\begin{eqnarray}r&=&P(2)\nonumber\\&=&2^2+3\times 2+1\nonumber\\&=&11\nonumber\end{eqnarray}として求められる筈である。
実際に、\(P(x)\) の割り算をしてみると、\begin{eqnarray}P(x)&=&x^2+3x+1\nonumber\\&=&(x-2)(x+5)+11\nonumber\end{eqnarray}となり、商が\((x-5)\)で、余り\(r\) は\(11\) となる。
多項式\(P(x)\)を\((x-a)\) で除したときの商を\(Q(x)\) 、剰余を\(r\) とおくと、\[P(x)=(x-a)Q(x)+r\]が成立しているところ、同式で、\(x=a\) としてみると、\begin{eqnarray}P(a)&=&(a-a)Q(a)+r\nonumber\\&=&0\times Q(a)+r\nonumber\\&=&r\nonumber\end{eqnarray}となる。よって、\(r\) は、\(P(a)\)として求められる。
s_1=x+y+z \\
s_2=xy+yz+zx\\
s_3=xyz
\end{array}\right.\]
\(s_1\) の三乗は、多項定理を用いて、\begin{eqnarray}(s_1)^3&=&(x+y+z)^3\nonumber\\&=&x^3+y^3+z^3\nonumber\\& &+3(x^2y+xy^2+y^2z+yz^2+x^2z+xz^2)\nonumber\\& &+6xyz\nonumber\end{eqnarray}となる。
例えば、\[(x+y+z)^3\]を展開したときの、\(xyz\) すなわち、\[x^1~y^1~z^1\]の係数は、\begin{eqnarray}\frac{3!}{1!~1!~1!}&=&\frac{3\times 2\times 1}{1}\nonumber\\&=&6\nonumber\end{eqnarray}である。また、\(x^2y\) すなわち、 \[x^2~y^1~z^0\]の係数は、\begin{eqnarray}\frac{3!}{2!~1!~0!}&=&\frac{3\times 2\times 1}{2\times 1 \times 1\times 1}\nonumber\\&=&3\nonumber\end{eqnarray}である。また、\(x^3\) すなわち、\[x^3~y^0~z^0\]の係数は、\begin{eqnarray}\frac{3!}{3!~0!~0!}&=&\frac{3\times 2\times 1}{3\times 2 \times 1\times 1\times 1}\nonumber\\&=&1\nonumber\end{eqnarray}となる。
https://www.amazon.co.jp/dp/4882299402/
p14 剰余定理
例えば、多項式 \(P(x)=x^2+3x+1\) を、\((x-2)\) で割った場合の剰余 \(r\) は、剰余定理によれば、\begin{eqnarray}r&=&P(2)\nonumber\\&=&2^2+3\times 2+1\nonumber\\&=&11\nonumber\end{eqnarray}として求められる筈である。
実際に、\(P(x)\) の割り算をしてみると、\begin{eqnarray}P(x)&=&x^2+3x+1\nonumber\\&=&(x-2)(x+5)+11\nonumber\end{eqnarray}となり、商が\((x-5)\)で、余り\(r\) は\(11\) となる。
p14 剰余定理の証明
p14 基本対称式
\[ \left\{\begin{array}{l}s_1=x+y+z \\
s_2=xy+yz+zx\\
s_3=xyz
\end{array}\right.\]
p14 s_1 の三乗
\(s_1\) の三乗は、多項定理を用いて、\begin{eqnarray}(s_1)^3&=&(x+y+z)^3\nonumber\\&=&x^3+y^3+z^3\nonumber\\& &+3(x^2y+xy^2+y^2z+yz^2+x^2z+xz^2)\nonumber\\& &+6xyz\nonumber\end{eqnarray}となる。
p14 多項定理
\[(A+B+C+\cdots +Z)^n\]を展開したときの、ある項\[A^a~B^b~C^c\cdots Z^z\]の係数は、\[\frac{n!}{a!~b!~c!\cdots z!}\]である。例えば、\[(x+y+z)^3\]を展開したときの、\(xyz\) すなわち、\[x^1~y^1~z^1\]の係数は、\begin{eqnarray}\frac{3!}{1!~1!~1!}&=&\frac{3\times 2\times 1}{1}\nonumber\\&=&6\nonumber\end{eqnarray}である。また、\(x^2y\) すなわち、 \[x^2~y^1~z^0\]の係数は、\begin{eqnarray}\frac{3!}{2!~1!~0!}&=&\frac{3\times 2\times 1}{2\times 1 \times 1\times 1}\nonumber\\&=&3\nonumber\end{eqnarray}である。また、\(x^3\) すなわち、\[x^3~y^0~z^0\]の係数は、\begin{eqnarray}\frac{3!}{3!~0!~0!}&=&\frac{3\times 2\times 1}{3\times 2 \times 1\times 1\times 1}\nonumber\\&=&1\nonumber\end{eqnarray}となる。
p14 s_1~s_2
\(s_1~s_2\)
\begin{eqnarray}s_1~s_2&=&(x+y+z)(xy+yz+zx)\nonumber\\&=&x^2y+xyz+x^2z\nonumber\\& &+xy^2+y^2z+xyz\nonumber\\&&+xyz+yz^2+xz^2\nonumber\\&=&x^2y+xy^2+y^2z+yz^2+x^2z+xz^2+3xyz\nonumber\end{eqnarray}
(参照:複素数の四則演算)
https://dbkids.co.jp/popimaging/seminar/complex/complexoperation.htm
ここで、\[\omega=\frac{\gamma-\beta}{\alpha-\beta}\]と置くと、上記式より、\[ \left\{\begin{array}{l}
|\omega|=1 \\
\arg(\omega)=\pm\frac{\pi}{3}
\end{array}\right.\]となる。
この\(\omega\) を別の複素数平面に図示すると、以下のように、大きさが \(1\) (すなわち絶対値を変更しない)、偏角が \(\pm\frac{\pi}{3}\) の座標変換として把握できる(\(\pm i~\sin(\frac{\pi}{3})\) のうち、\(i~\sin(\frac{\pi}{3})\) を描画)。
図から、その正負の符号はマイナスであるから、\(\omega^2-\omega=-1\) となる。すなわち、\(\omega\) は、以下の式をみたす。\[\omega^2-\omega+1=0\]この\(\omega\) を元の表記に戻すと、\[\left(\frac{\gamma-\beta}{\alpha-\beta}\right)^2-\frac{\gamma-\beta}{\alpha-\beta}+1=0\]となる。
\(f(x)\) を\((2x+3)\) で割ったときの余りが\(6\) であるから、商を\(g(x)\) とすれば、以下の等式が成立する。\[f(x)=(2x+3)g(x)+6\]同様に、\((3x+7)f(x)\) を\((2x+3)\) で割ったときの余りを\(r\) 、商を\(h(x)\) とすれば、以下の等式が成立する。\[(3x+7)f(x)=(2x+3)h(x)+r\]ここで、\(x=-\frac{3}{2}\) を代入すると、上式は、\begin{eqnarray}f\left(\frac{-3}{2}\right)&=&\left(2\times \frac{-3}{2}+3\right)~g\left(\frac{-3}{2}\right)+6\nonumber\\&=&0\times g\left(\frac{-3}{2}\right)+6\nonumber\\&=&6\nonumber\end{eqnarray}同様に下式に、\(x=-\frac{3}{2}\) を代入すると、\begin{eqnarray}\left(3\times \frac{-3}{2}+7\right)\times f\left(\frac{-3}{2}\right)&=&\left(2\times\frac{-3}{2}+3\right)h\left(\frac{-3}{2}\right)+r\nonumber\\ \left(\frac{-9}{2}+7\right)\times f\left(\frac{-3}{2}\right)&=&0\times h\left(\frac{-3}{2}\right)+r\nonumber\\ \frac{-9+14}{2}\times f\left(\frac{-3}{2}\right)&=&r\nonumber\\r&=&\frac{-9+14}{2}\times f\left(\frac{-3}{2}\right)\nonumber\\&=&\frac{5}{2}\times f\left(\frac{-3}{2}\right)\nonumber\\&=&\frac{5}{2}\times 6\nonumber\\&=&15\nonumber\end{eqnarray}
\(x^2-4=(x+2)(x-2)\) であることから、与式を、以下のような部分分数の形へと変形することを考える(\(A,~B\)は未定係数)。\[\frac{1}{x^2-4}=\frac{A}{x+2}+\frac{B}{x-2}\]右辺は、以下のように変形できるので、\begin{eqnarray}&=&\frac{A}{x+2}+\frac{B}{x-2}\nonumber\\&=&\frac{A(x-2)+B(x+2)}{(x+2)(x-2)}\nonumber\\&=&\frac{(A+B)x-2A+2B}{x^2-4}\nonumber\end{eqnarray}与式は、以下のようになる。\[\frac{1}{x^2-4}=\frac{(A+B)x-2A+2B}{x^2-4}\]分子どおしを比較すると、どのような \(x\) に対しても、同式が成立するためには、以下の連立方程式を充たす必要があることが分かる。\[ \left\{\begin{array}{l}
A+B=0 \\
-2A+2B=1
\end{array}\right.\]これを解くと、\[ \left\{\begin{array}{l}
A=-\frac{1}{4} \\
B=\frac{1}{4}
\end{array}\right.\]となるので、与式は、以下の部分分数の形に変形できる。\begin{eqnarray}\frac{1}{x^2-4}&=&\frac{-1}{4(x+2)}+\frac{1}{4(x-2)}\nonumber\\&=& \frac{1}{4}\left(\frac{-1}{x+2}+\frac{1}{x-2}\right)\nonumber\\&=&\frac{1}{4}\left(\frac{1}{x-2}-\frac{1}{x+2}\right)\nonumber\end{eqnarray}
複素数 \(z=x+iy\) の偏角を \(\theta\) とすると、複素数の乗算により得られた新たな複素数の偏角は、元の2つの複素数の各々の偏角の和であるから、\(z^2\) の偏角は、\(\theta+\theta=2\theta\) である。他方、複素数 \(z\) の共役複素数 \(\bar{z}=x-iy\) は、\(x\) 軸について \(z\) と線対称なので、その偏角は\(-\theta\) である。これらが等しいというのであるから、\begin{eqnarray}2\theta&=&-\theta\nonumber\end{eqnarray}を充たすような\(\theta\) を求めれば良い。
\begin{eqnarray}s_1~s_2&=&(x+y+z)(xy+yz+zx)\nonumber\\&=&x^2y+xyz+x^2z\nonumber\\& &+xy^2+y^2z+xyz\nonumber\\&&+xyz+yz^2+xz^2\nonumber\\&=&x^2y+xy^2+y^2z+yz^2+x^2z+xz^2+3xyz\nonumber\end{eqnarray}
p15 複素平面上の三角形
正三角形は各辺の長さが等しいことから、\[\frac{|\gamma-\beta|}{|\alpha-\beta|}=1\]また、正三角形のひとつの内角は\(\frac{\pi}{3}\) であることから、\[\angle \alpha\beta\gamma=\pm\frac{\pi}{3}\]である。複素数の除算により得られた新たな複素数の偏角は、元の2つの複素数の各々の偏角の差であるから、同式は、\[\arg\left(\frac{\gamma-\beta}{\alpha-\beta}\right)=\pm\frac{\pi}{3}\]のように表現できる。(参照:複素数の四則演算)
https://dbkids.co.jp/popimaging/seminar/complex/complexoperation.htm
ここで、\[\omega=\frac{\gamma-\beta}{\alpha-\beta}\]と置くと、上記式より、\[ \left\{\begin{array}{l}
|\omega|=1 \\
\arg(\omega)=\pm\frac{\pi}{3}
\end{array}\right.\]となる。
この\(\omega\) を別の複素数平面に図示すると、以下のように、大きさが \(1\) (すなわち絶対値を変更しない)、偏角が \(\pm\frac{\pi}{3}\) の座標変換として把握できる(\(\pm i~\sin(\frac{\pi}{3})\) のうち、\(i~\sin(\frac{\pi}{3})\) を描画)。
次に、\(\omega^2\) について検討をする。複素数の乗算により得られた新たな複素数の偏角は、元の2つの複素数の各々の偏角の和であるから、\(\omega^2\) すなわち \(\omega\times \omega\) は、同じ反時計回り方向への\(\frac{\pi}{3}\) を2回おこなったもの、すなわち、\(\frac{2\pi}{3}\) 回転を意味することになる。
ここで、\(\omega\) の先端と \(\omega^2\) の先端と原点との三点からなる三角形を考えると、原点での角の角度差は、\(\frac{\pi}{3}\) であり、また、\(|\omega|=|\omega^2|=1\) であるから、同三角形は正三角形をなす。よって、\(\omega\) の先端と \(\omega^2\) の先端とを結んだ辺も他の辺と同様、長さ\(1\) となる。すなわち、以下の図において、\(|\omega^2-\omega|=1\) となる。
p16 計算技能問題2
\(f(x)\) を\((2x+3)\) で割ったときの余りが\(6\) であるから、商を\(g(x)\) とすれば、以下の等式が成立する。\[f(x)=(2x+3)g(x)+6\]同様に、\((3x+7)f(x)\) を\((2x+3)\) で割ったときの余りを\(r\) 、商を\(h(x)\) とすれば、以下の等式が成立する。\[(3x+7)f(x)=(2x+3)h(x)+r\]ここで、\(x=-\frac{3}{2}\) を代入すると、上式は、\begin{eqnarray}f\left(\frac{-3}{2}\right)&=&\left(2\times \frac{-3}{2}+3\right)~g\left(\frac{-3}{2}\right)+6\nonumber\\&=&0\times g\left(\frac{-3}{2}\right)+6\nonumber\\&=&6\nonumber\end{eqnarray}同様に下式に、\(x=-\frac{3}{2}\) を代入すると、\begin{eqnarray}\left(3\times \frac{-3}{2}+7\right)\times f\left(\frac{-3}{2}\right)&=&\left(2\times\frac{-3}{2}+3\right)h\left(\frac{-3}{2}\right)+r\nonumber\\ \left(\frac{-9}{2}+7\right)\times f\left(\frac{-3}{2}\right)&=&0\times h\left(\frac{-3}{2}\right)+r\nonumber\\ \frac{-9+14}{2}\times f\left(\frac{-3}{2}\right)&=&r\nonumber\\r&=&\frac{-9+14}{2}\times f\left(\frac{-3}{2}\right)\nonumber\\&=&\frac{5}{2}\times f\left(\frac{-3}{2}\right)\nonumber\\&=&\frac{5}{2}\times 6\nonumber\\&=&15\nonumber\end{eqnarray}
p16 計算技能問題4(1)
\(x^2-4=(x+2)(x-2)\) であることから、与式を、以下のような部分分数の形へと変形することを考える(\(A,~B\)は未定係数)。\[\frac{1}{x^2-4}=\frac{A}{x+2}+\frac{B}{x-2}\]右辺は、以下のように変形できるので、\begin{eqnarray}&=&\frac{A}{x+2}+\frac{B}{x-2}\nonumber\\&=&\frac{A(x-2)+B(x+2)}{(x+2)(x-2)}\nonumber\\&=&\frac{(A+B)x-2A+2B}{x^2-4}\nonumber\end{eqnarray}与式は、以下のようになる。\[\frac{1}{x^2-4}=\frac{(A+B)x-2A+2B}{x^2-4}\]分子どおしを比較すると、どのような \(x\) に対しても、同式が成立するためには、以下の連立方程式を充たす必要があることが分かる。\[ \left\{\begin{array}{l}
A+B=0 \\
-2A+2B=1
\end{array}\right.\]これを解くと、\[ \left\{\begin{array}{l}
A=-\frac{1}{4} \\
B=\frac{1}{4}
\end{array}\right.\]となるので、与式は、以下の部分分数の形に変形できる。\begin{eqnarray}\frac{1}{x^2-4}&=&\frac{-1}{4(x+2)}+\frac{1}{4(x-2)}\nonumber\\&=& \frac{1}{4}\left(\frac{-1}{x+2}+\frac{1}{x-2}\right)\nonumber\\&=&\frac{1}{4}\left(\frac{1}{x-2}-\frac{1}{x+2}\right)\nonumber\end{eqnarray}
p16 計算技能問題7
複素数 \(z=x+iy\) の偏角を \(\theta\) とすると、複素数の乗算により得られた新たな複素数の偏角は、元の2つの複素数の各々の偏角の和であるから、\(z^2\) の偏角は、\(\theta+\theta=2\theta\) である。他方、複素数 \(z\) の共役複素数 \(\bar{z}=x-iy\) は、\(x\) 軸について \(z\) と線対称なので、その偏角は\(-\theta\) である。これらが等しいというのであるから、\begin{eqnarray}2\theta&=&-\theta\nonumber\end{eqnarray}を充たすような\(\theta\) を求めれば良い。
そのような \(\theta\) は、上記図より、\[\theta=\frac{2}{3}\pi\]である。これを複素数で表示すると、\begin{eqnarray}z&=&\cos\frac{2}{3}\pi\pm i~\sin\frac{2}{3}\pi\nonumber\\&=&-\frac{1}{2}\pm i~\frac{\sqrt{1^2-\left(\frac{1}{2}\right)^2}}{1}\nonumber\\&=&-\frac{1}{2}\pm i~\sqrt{\frac{3}{4}}\nonumber\\&=& -\frac{1}{2}\pm i~\frac{\sqrt{3}}{2}\nonumber\end{eqnarray}
となる。
このほか、\(\theta\) が、ちょうど一回転となる場合(\(\theta=0,~2\pi,~\cdots 2n\pi\))も、常に、\(z^2=\bar{z}\) となるので、解となる。その複素数表示は、\begin{eqnarray}z&=&1+i\times 0\nonumber\\&=&1\nonumber\end{eqnarray}である。更に、\(z\) が回転変換ではなく、常に原点\((0,0)\) へと原像を移動させる変換である場合、\(\bar{z}\) による写像も常に原点\((0,0)\) へと原像を移動させるという点で一致することになるので、解となる。その複素数表示は、
\begin{eqnarray}z&=&0+i\times 0\nonumber\\&=&0\nonumber\end{eqnarray}である。
p18 例1
関数 \(f(x)=\log_{10}(x)\) のグラフより、領域\(1<x\) において、\(\log_{10}(x)\) は常に正。
すなわち、\(0<\log_{10}2\) である。そこで、仮に正の整数 \(m,~n\) を用いて、\[\log_{10}2=\frac{n}{m}\]と表し得るかを検討する(他の場合、すなわち、\(n=0\) の場合は \(\log_{10}2=0\) となり誤りであり成り立たない。\(m=0\) の場合は\(0\) 除算となり定義できないので成り立たない。また、\(m, ~n\) のいずれかが負の整数である場合は \(\log_{10}2<0\) となり誤りであり成り立たない。\(m, ~n\) のいずれもが負の整数である場合は、いずれもが正である場合の検討で置き換えることができるので、独立に検討する意味がない)。
与式を変形すると、\begin{eqnarray}\log_{10}2&=&\frac{n}{m}\nonumber\\2&=&10^{\frac{n}{m}}\nonumber\\2^m&=&(10^{\frac{n}{m}})^m\nonumber\\2^m&=&10^n\nonumber\\ \frac{2^m}{2^n}&=&\frac{10^n}{2^n}\nonumber\\2^{m-n}&=&5^n\nonumber\end{eqnarray}となる。しかし、同式の左辺は偶数、右辺は奇数であるから、同等式は成立しない。(\(m-n=0,~n=0\) であれば、左辺・右辺ともに\(1\) となり成立するが、\(n\) は正の整数であるから、その余地はない。)よって、\(\log_{10}2\) は、整数 \(m, ~n\) を用いて、\(\frac{n}{m}\) の形で表し得る数(有理数)ではない。すなわち、無理数である。
p19 計算技能問題3
\begin{eqnarray}\cos\theta+\sin\theta&=&\frac{1}{2}\nonumber\\(\cos\theta+\sin\theta)^2&=&\left(\frac{1}{2}\right)^2\nonumber\\ \cos^2\theta+2\cos\theta\sin\theta+\sin^2\theta&=&\frac{1}{4}\nonumber\\1+2\cos\theta\sin\theta&=&\frac{1}{4}\nonumber\\2\cos\theta\sin\theta&=&-\frac{3}{4}\nonumber\\ \cos\theta\sin\theta&=&-\frac{3}{8}\nonumber\end{eqnarray}
p19 計算技能問題5
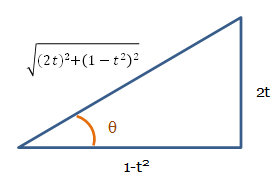
\begin{eqnarray}\tan\theta&=&\frac{\tan\frac{\theta}{2}+\tan\frac{\theta}{2}}{1-\tan\frac{\theta}{2}\cdot\tan\frac{\theta}{2}}\nonumber\\&=&\frac{t+t}{1-t\cdot t}\nonumber\\&=&\frac{2t}{1-t^2}\nonumber\end{eqnarray}
よって、\(\theta\) を含む三角形の各辺の関係は、以下の図のようになる。
\begin{eqnarray}\sin\theta&=&\frac{2t}{\sqrt{(2t)^2+(1-t^2)^2}}\nonumber\\&=&\frac{2t}{\sqrt{4t^2+t^4-2t^2+1}}\nonumber\\&=&\frac{2t}{\sqrt{t^4+2t^2+1}}\nonumber\\&=&\frac{2t}{\sqrt{(t^2+1)^2}}\nonumber\\&=&\frac{2t}{t^2+1}\nonumber\end{eqnarray}同様にして、\begin{eqnarray}\cos\theta&=&\frac{1-t^2}{\sqrt{(2t)^2+(1-t^2)^2}}\nonumber\\&=&\frac{1-t^2}{1+t^2}\nonumber\end{eqnarray}
p20 楕円の方程式
p20 例1
\begin{eqnarray}r&=&\frac{1}{1+\cos\theta}\nonumber\\r(1+\cos\theta)&=&1\nonumber\\r+r\cos\theta&=&1\nonumber\\r&=&1-r\cos\theta\nonumber\\r&=&1-x\nonumber\\r^2&=&(1-x)^2\nonumber\end{eqnarray}他方で、\begin{eqnarray}x^2+y^2&=&(r\cos\theta)^2+(r\cos\theta)^2\nonumber\\&=&r^2(\cos^2\theta+\sin^2\theta)\nonumber\\&=&r^2\nonumber\end{eqnarray}よって、\begin{eqnarray}(1-x)^2&=&x^2+y^2\nonumber\\1-2x+x^2&=&x^2+y^2\nonumber\\1-2x&=&y^2\nonumber\\-2x&=&y^2-1\nonumber\\x&=&-\frac{1}{2}y^2+\frac{1}{2}\nonumber\end{eqnarray}となる。これは、点(\(\frac{1}{2},~0\))を通る\(x\)軸に上に突の放物線である。
p21 例2
回転座標系の変換式の導出について
(参考:高校物理の備忘録 https://physnotes.jp/mechanics/2d_rot_cor/)
p21 例3
だ円の媒介変数表示について
p21 例3(直交する二直線)
二直線が直交する場合、各々の方向ベクトルも直交するから、方向ベクトルの内積は \(0\) である。よって、\[ \left\{\begin{array}{l}a_1x+b_1y=0 \\a_2x+b_2y=0\end{array}\right.\]すなわち、\[ \left\{\begin{array}{l}y=-\frac{a_1}{b_1}x \\y=-\frac{a_2}{b_2}x\end{array}\right.\]が直交するとき、方向ベクトル \((b_1,-a_1),~(b_2,-a_2)\) について、その内積が\(0\) となるから、\begin{eqnarray}b_1b_2+(-a_1)(-a_2)&=&0\nonumber\\b_1b_2+a_1a_2&=&0\nonumber\\a_1a_2&=&-b_1b_2\nonumber\\a_2&=&-\frac{b_1b_2}{a_1}\nonumber\end{eqnarray}となる。これを上記第2式に代入すると、\begin{eqnarray}a_2x+b_2y&=&0\nonumber\\-\frac{b_1b_2}{a_1}x+b_2y&=&0\nonumber\\-\frac{b_1}{a_1}x+y&=&0\nonumber\\-b_1x+a_1y&=&0\nonumber\\b_1x-a_1y&=&0\nonumber\end{eqnarray}となる。よって、二直線\[ \left\{\begin{array}{l}ax+by=0 \\bx-ay=0\end{array}\right.\]は直交する。例えば、二直線\[ \left\{\begin{array}{l}2x+5y=0 \\5x-2y=0\end{array}\right.\]は、各々、傾きが \(-\frac{2}{5},~\frac{5}{2}\) の直線であり、以下のように直交する。
交点の座標は、上記連立方程式を解いた解であり、\((0,0)\) となる。
切片定数がついた場合でも、同様であり、例えば、二直線\[ \left\{\begin{array}{l}2x+5y+3=0 \\5x-2y-7=0\end{array}\right.\]は、以下のように直交する。
交点の座標は、上記連立方程式を解いた解であり、\((1,-1)\) となる。
p21 例3(ある直線に垂直で、かつ、特定の点を通る直線)
いま、\[ax+by+c=0\]に垂直な直線として、\[bx-ay=0\]が考えられる。
同直線が点\((x_0,~y_0)\) を通るとき、同式は、\[b(x-x_0)-a(y-y_0)=0\]となる。なお、両直線の交点の座標は、連立方程式\[ \left\{\begin{array}{l}ax+by+c=0 \\b(x-x_0)-a(y-y_0)=0\end{array}\right.\]を \(x,~y\) について解くことで得られる。
p21 例3(接線に引いた垂線の交点 H の座標)
接線の方程式は、\[\frac{\cos\theta}{a}x+\frac{\sin\theta}{b}y-1=0\]であり、同接線に垂直で、かつ、点(\(c,~0\))を通る直線は、\[\frac{\sin\theta}{b}(x-c)-\frac{\cos\theta}{a}(y-0)=0\]であるから、両直線の交点 H の座標 \((x,~y)\) は、両式を連立方程式\[ \left\{\begin{array}{l}\frac{\cos\theta}{a}x+\frac{\sin\theta}{b}y-1=0 \\ \frac{\sin\theta}{b}(x-c)-\frac{\cos\theta}{a}(y-0)=0\end{array}\right.\]としたときの解として得られる。第1式を変形すると、\begin{eqnarray}\frac{\cos\theta}{a}x+\frac{\sin\theta}{b}y&=&1\nonumber\\b\cos\theta~ x+a\sin\theta~y&=&ab\nonumber\end{eqnarray}となり、第2式を変形すると、\begin{eqnarray}\frac{\sin\theta}{b}x-\frac{\cos\theta}{a}y&=&\frac{c}{b}\sin\theta\nonumber\\a\sin\theta~x-b\cos\theta~y&=&ac\sin\theta\nonumber\end{eqnarray}となるので、連立方程式は、\[ \left\{\begin{array}{l}b\cos\theta~x+a\sin\theta~y=ab\\a\sin\theta~x-b\cos\theta~y=ac\sin\theta\end{array}\right.\]となる。
これを、\((x,~y)\) について解くために、行列形式で表わすと、\[ \left( \begin{array}{ccc} b\cos\theta & a\sin\theta \\ a\sin\theta & -b\cos\theta \end{array} \right)\left(\begin{array}{ccc}x\\y\end{array}\right)=\left(\begin{array}{ccc}ab\\ac\sin\theta\end{array}\right)\]となる。
両辺に左から、逆行列を乗ずると、\begin{eqnarray}\left(\begin{array}{ccc}x\\y\end{array}\right)&=&\frac{1}{-b^2\cos^2\theta-a^2\sin^2\theta}\left(\begin{array}{ccc}-b\cos\theta&-a\sin\theta\\-a\sin\theta&b\cos\theta\end{array}\right)\left(\begin{array}{ccc}ab\\ac\sin\theta\end{array}\right)\nonumber\\&=&\frac{1}{b^2\cos^2\theta+a^2\sin^2\theta}\left(\begin{array}{ccc}b\cos\theta&a\sin\theta\\a\sin\theta&-b\cos\theta\end{array}\right)\left(\begin{array}{ccc}ab\\ac\sin\theta\end{array}\right)\nonumber\\&=&\frac{1}{b^2\cos^2\theta+a^2\sin^2\theta}\left(\begin{array}{ccc}ab^2\cos\theta+a^2c\sin^2\theta\\a^2b\sin\theta-abc\sin\theta\cos\theta\end{array}\right)\nonumber\\&=&\frac{1}{a^2\sin^2\theta+b^2\cos^2\theta}\left(\begin{array}{ccc}a(b^2\cos\theta+ac\sin^2\theta)\\ab\sin\theta(a-c\cos\theta)\end{array}\right)\nonumber\end{eqnarray}となるので、
交点Hの座標 \((x,~y)\) が、\[x=\frac{a(b^2\cos\theta+ac\sin^2\theta)}{a^2\sin^2\theta+b^2\cos^2\theta}\]\[y=\frac{ab\sin\theta(a-c\cos\theta)}{a^2\sin^2\theta+b^2\cos^2\theta}\]として求められた。
p21 例3( H の軌跡が円となることの証明)
点Hの座標\((x,~y)\) について、\begin{eqnarray}x^2+y^2&=&\left(\frac{a(b^2\cos\theta+ac\sin^2\theta)}{a^2\sin^2\theta+b^2\cos^2\theta}\right)^2+\left(\frac{ab\sin\theta(a-c\cos\theta)}{a^2\sin^2\theta+b^2\cos^2\theta}\right)^2\nonumber\\&=&\frac{a^2(b^4\cos^2\theta+2ab^2c\cos\theta\sin^2\theta+a^2c^2\sin^4\theta)}{(a^2\sin^2\theta+b^2\cos^2\theta)^2}\nonumber\\& &+\frac{a^2b^2\sin^2\theta(a^2-2ac\cos\theta+c^2\cos^2\theta)}{(a^2\sin^2\theta+b^2\cos^2\theta)^2}\nonumber\\&=& \frac{a^2b^4\cos^2\theta+2a^3b^2c\cos\theta\sin^2\theta+a^4c^2\sin^4\theta}{(a^2\sin^2\theta+b^2\cos^2\theta)^2}\nonumber\\& &+\frac{a^4b^2\sin^2\theta-2a^3b^2c\cos\theta\sin^2\theta+a^2b^2c^2\sin^2\theta\cos^2\theta}{(a^2\sin^2\theta+b^2\cos^2\theta)^2}\nonumber\\&=& \frac{a^2b^4\cos^2\theta+a^4c^2\sin^4\theta+a^4b^2\sin^2\theta+a^2b^2c^2\sin^2\theta\cos^2\theta}{(a^2\sin^2\theta+b^2\cos^2\theta)^2}\nonumber\\&=& \frac{a^2b^2(b^2\cos^2\theta+a^2\sin^2\theta)+a^2c^2\sin^2\theta(a^2\sin^2\theta+b^2\cos^2\theta)}{(a^2\sin^2\theta+b^2\cos^2\theta)^2}\nonumber\\&=& \frac{a^2b^2+a^2c^2\sin^2\theta}{a^2\sin^2\theta+b^2\cos^2\theta}\nonumber\\&=& \frac{a^2(b^2+c^2\sin^2\theta)}{a^2\sin^2\theta+b^2\cos^2\theta}\nonumber\end{eqnarray}となるところ、\[c^2=a^2-b^2\]を代入すると、与式は、\begin{eqnarray}&=&\frac{a^2(b^2+(a^2-b^2)\sin^2\theta)}{a^2\sin^2\theta+b^2\cos^2\theta}\nonumber\\&=&\frac{a^2(b^2+a^2\sin^2\theta-b^2\sin^2\theta)}{a^2\sin^2\theta+b^2\cos^2\theta}\nonumber\\&=&\frac{a^2(a^2\sin^2\theta+b^2(1-\sin^2\theta))}{a^2\sin^2\theta+b^2\cos^2\theta}\nonumber\\&=&\frac{a^2(a^2\sin^2\theta+b^2\cos^2\theta)}{a^2\sin^2\theta+b^2\cos^2\theta}\nonumber\\&=&a^2\nonumber\end{eqnarray}となる。
すなわち、\[x^2+y^2=a^2\]となる。
これは、原点\((0,~0)\) を中心とする半径\(a\) の円を表している。
p21 例4
\[\cos^2t=\frac{1}{1+\tan^2t}\]の関係を式変形に用いている。同式の証明は、以下のとおり。\begin{eqnarray}\cos^2t+\sin^2t&=&1\nonumber\\ \left(1+\frac{\sin^2t}{\cos^2t}\right)\cos^2t&=&1\nonumber\\(1+\tan^2t)\cos^2t&=&1\nonumber\\\cos^2t&=&\frac{1}{1+\tan^2t}\nonumber\end{eqnarray}