「統計解析のはなし―データに語らせるテクニック」7章
大村平「統計解析のはなし―データに語らせるテクニック」日科技連 の読後行間補充メモ
同書籍は、印刷数表と手計算による統計解析を紹介した良書。
本稿では、同書籍の設例について、プログラムによる演算処理をした場合の例を示す。
コードと出力例は、Python[Google Colaboratory]
7章 総身に知恵はまわるのか ~相関と回帰のはなし~
p201~204 正の相関/負の相関/相関なし
import pandas as pd
index_info = ['By_Kou','By_Otsu'] # 共通
col_info = ['A','B','C','D','E'] # 共通
# 表7.1
DF = pd.DataFrame([[5,4,3,2,1], [5,4,3,2,1]],
index = index_info, columns = col_info)
DF.loc['multiplied'] = DF.loc['By_Kou'] * DF.loc['By_Otsu']
squared_sum = DF.loc['multiplied'].sum()
print(f'表7.1\n{DF}')
print(f'積和:{squared_sum}')
# 表7.2
DF2 = pd.DataFrame([[5,4,3,2,1], [1,2,3,4,5]],
index = index_info, columns = col_info)
DF2.loc['multiplied'] = DF2.loc['By_Kou'] * DF2.loc['By_Otsu']
squared_sum = DF2.loc['multiplied'].sum()
print(f'\n表7.2\n{DF2}')
print(f'積和:{squared_sum}')
# 表7.3
DF3 = pd.DataFrame([[5,4,3,2,1], [4,1,3,5,2]],
index = index_info, columns = col_info)
DF3.loc['multiplied'] = DF3.loc['By_Kou'] * DF3.loc['By_Otsu']
squared_sum = DF3.loc['multiplied'].sum()
print(f'\n表7.3\n{DF3}')
print(f'積和:{squared_sum}')
表7.1
A B C D E
By_Kou 5 4 3 2 1
By_Otsu 5 4 3 2 1
multiplied 25 16 9 4 1
積和:55
表7.2
A B C D E
By_Kou 5 4 3 2 1
By_Otsu 1 2 3 4 5
multiplied 5 8 9 8 5
積和:35
表7.3
A B C D E
By_Kou 5 4 3 2 1
By_Otsu 4 1 3 5 2
multiplied 20 4 9 10 2
積和:45
p207 表7.4
順位の相関を求めるための数表
import pandas as pd # 関数の定義 def max_calc(number): # 最大値 return(number*(number+1)*(2*number+1)/6) def mini_calc(number): # 最小値 return(number*(number+1)*(number+2)/6) def median_calc(number): # 中央値 return((max_calc(number)+mini_calc(number))/2) def divise_calc(number): # 除数 return(max_calc(number) -median_calc(number)) # 項目用空リスト numbers = [] max = [] min = [] deduct = [] divisor = [] # 各項目を関数で計算して、リストに格納 for n in range(2, 9, 1): # n を2~8で生成 numbers.append(n) max.append(max_calc(n)) min.append(mini_calc(n)) deduct.append(median_calc(n)) divisor.append(divise_calc(n)) DF = pd.DataFrame([numbers,max,min,deduct,divisor]).T # 結果をDFに整理 DF.columns=['Number','Max','Min','Deduct','Divisor'] DF # 表7.4
Number Max Min Deduct Divisor 0 2.0 5.0 4.0 4.5 0.5 1 3.0 14.0 10.0 12.0 2.0 2 4.0 30.0 20.0 25.0 5.0 3 5.0 55.0 35.0 45.0 10.0 4 6.0 91.0 56.0 73.5 17.5 5 7.0 140.0 84.0 112.0 28.0 6 8.0 204.0 120.0 162.0 42.0
p210 図7.1 順位相関を目で見る 表7.1の場合
# 図7.1
import pandas as pd
import matplotlib.pyplot as plt
index_info = ['By_Kou','By_Otsu']
col_info = ['A','B','C','D','E']
# 表7.1
DF71 = pd.DataFrame([[5,4,3,2,1], [5,4,3,2,1]],
index = index_info, columns = col_info)
y = DF71.loc['By_Kou'] # グラフxデータ
x = DF71.loc['By_Otsu'] # グラフyデータ
plt.scatter(x, y,s=300)
plt.xlabel(index_info[1])
plt.ylabel(index_info[0])
plt.plot([3, 3], [0, 6], color="black") #縦線 x=3
plt.plot([0, 6], [3, 3], color="black") #横線 y=3
plt.grid(True)
plt.title('Chart_71')
plt.show()
p210 図7.1 順位相関を目で見る 208頁の場合
# コードは上記の続き
DF208 = pd.DataFrame([[5,4,3,2,1], [4,3,5,1,2]],
index = index_info, columns = col_info)
y = DF208.loc['By_Kou'] # グラフxデータ
x = DF208.loc['By_Otsu'] # グラフyデータ
plt.scatter(x, y,s=300)
plt.xlabel(index_info[1])
plt.ylabel(index_info[0])
plt.plot([3, 3], [0, 6], color="black") #縦線 x=3
plt.plot([0, 6], [3, 3], color="black") #横線 y=3
plt.grid(True)
plt.title('Chart_208')
p211 相関係数 表7.5
学科得点とスポーツ成績の相関
import pandas as pd
import math
import matplotlib.pyplot as plt
# 基礎データ
index_info = ['Academics_Score','Sports_Score']
col_info = ['A','B','C','D','E','F']
DF75 = pd.DataFrame([[6,5,9,9,6,7], [5,5,7,8,4,7]],
index = index_info, columns = col_info)
DF75T = DF75.T
DF75T
p213 図7.3 座標の原点をデータの中心へ
第1象限と第3象限にある点は、\(x\times y\) 値がプラスになる(正の相関判定に利用)。
# グラフ化
x = DF75.loc['Academics_Score']
y = DF75.loc['Sports_Score']
plt.scatter(x, y,s=200)
plt.xlabel('Academics_Score')
plt.ylabel('Sports_Score')
# 平均線
x_ave = DF75.loc['Academics_Score'].mean()
y_ave = DF75.loc['Sports_Score'].mean()
plt.plot([x_ave, x_ave], [0, 10], color="black") #縦線 xの平均
plt.plot([0, 10], [y_ave, y_ave], color="black") #横線 yの平均
plt.grid(True)
plt.title('Chart_71')
plt.show()
p215 表7.6 相関係数を求めるために
# 前提計算
DF75T['A_deviation'] = DF75T['Academics_Score']-x_ave
DF75T['S_deviation'] = DF75T['Sports_Score']-y_ave
DF75T['A_dev_squ'] = DF75T['A_deviation']**2
DF75T['S_dev_squ'] = DF75T['S_deviation']**2
DF75T['numerator'] = DF75T['A_deviation'] *DF75T['S_deviation']
DF75R = DF75T.reindex(columns=['Academics_Score', 'A_deviation', 'A_dev_squ','Sports_Score', 'S_deviation', 'S_dev_squ','numerator']) #列の並びを変更
DF75R.loc['Sum'] = DF75R.sum()
# 相関係数
Denominator = math.sqrt(DF75R['A_dev_squ']['Sum'] *DF75R['S_dev_squ']['Sum'])
Numerator = DF75R['numerator']['Sum']
Corr = Numerator/Denominator
print(f'correlation:{round(Corr,3)}')
# DFの表示
DF75R
p215 Pandas の関数 corr を使用した場合
# 既存関数での計算
import pandas as pd
Academic = pd.Series([6,5,9,9,6,7])
Sports = pd.Series ([5,5,7,8,4,7])
res = Academic.corr(Sports)
print(f'correlation:{round(res,3)}')
correlation:0.849
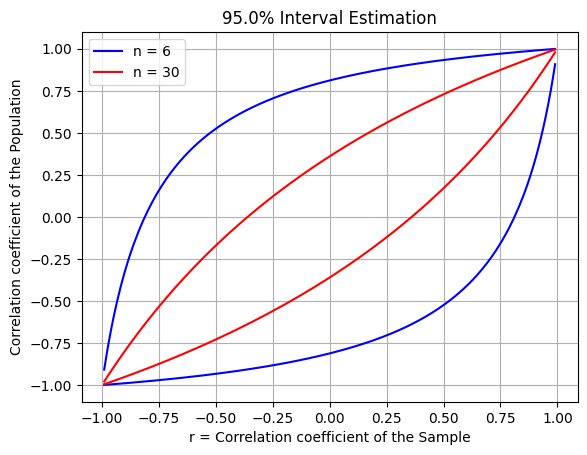
p216 相関係数の区間推定
標本から求めた相関係数 →母集団における相関係数を区間推定
import math
from scipy.stats import norm
import matplotlib.pyplot as plt
alpha = 0.05 # 危険率
n6 = 6 # 標本数
n30 = 30 # 標本数
# 関数 フィッシャーの z変換
def fisher(ratio): #標本の相関係数
z2 = math.log((1+ratio)/(1-ratio))
return z2/2
# 関数 確率 →パーセント値
def p_value(alpha): # 危険率
percent = norm.ppf(q = 1-alpha/2, loc=0) # 正規分布のp%点
return percent # パーセント値
# 母集団の相関係数の上側
def Upper(ratio, alpha, numbers): # 標本の相関係数、危険率、標本数
zvalue = fisher(ratio) # フィッシャーの z 変換関数を使用
percent = p_value(alpha) # パーセント値を求める関数を使用
up = zvalue + percent * math.sqrt(1/(numbers-3))
Upper= (math.exp(2*up)-1)/(math.exp(2*up)+1) # 上側を求める関数
return Upper
# 母集団の相関係数の下側
def Lower(ratio,alpha,numbers): # 標本の相関係数、危険率、標本数
zvalue = fisher(ratio)
percent = p_value(alpha)
low = zvalue - percent * math.sqrt(1/(numbers-3))
Low= (math.exp(2*low)-1)/(math.exp(2*low)+1)
return Low
# グラフ用データ列を用意
x_row = []
y6_u_row = [] # 標本数6の場合の上限データ用
y6_l_row = [] # 標本数6の場合の下限データ用
y30_u_row = []
y30_l_row = []
for rate in range(-99,100,1):
x_row.append(rate/100)
y6_u_row.append(Upper(rate/100,alpha,n6)) # 上限関数で計算
y6_l_row.append(Lower(rate/100,alpha,n6)) # 下限関数で計算
y30_u_row.append(Upper(rate/100,alpha,n30))
y30_l_row.append(Lower(rate/100,alpha,n30))
# 色を指定
colors = ["blue", "blue", "red", "red"]
plt.gca().set_prop_cycle(color=colors)
# グラフを描画
plt.plot(x_row, y6_u_row, label=f'n = {n6}') # 標本数6の上側グラフ
plt.plot(x_row, y6_l_row) # 標本数6の下側グラフ
plt.plot(x_row, y30_u_row, label=f'n = {n30}')
plt.plot(x_row, y30_l_row)
plt.grid() # 罫線
plt.title(f'{(1-alpha)*100}% Interval Estimation') # 表題
plt.xlabel("r = Correlation coefficient of the Sample") # x軸の名称
plt.ylabel("Correlation coefficient of the Population")
plt.legend() # 凡例
plt.show()
p217~218 事例
# 事例
ratio = 0.85 # 217頁設例
numbers = n6
up6_95 = Upper(ratio,alpha,numbers)
lo6_95 = Lower(ratio,alpha,numbers)
print(f'標本数{numbers}で相関係数{ratio}のとき、母集団の相関係数の{(1-alpha)*100}%信頼区間は、{round(lo6_95,2)}~{round(up6_95,2)}')
ratio = 0.85
numbers = 50 # 217頁設例
up50_95 = Upper(ratio,alpha,numbers)
lo50_95 = Lower(ratio,alpha,numbers)
print(f'標本数{numbers}で相関係数{ratio}のとき、母集団の相関係数の{(1-alpha)*100}%信頼区間は、{round(lo50_95,2)}~{round(up50_95,2)}')
ratio = 0.81 # 218頁設例
numbers = n6
up6_95 = Upper(ratio,alpha,numbers)
lo6_95 = Lower(ratio,alpha,numbers)
print(f'標本数{numbers}で相関係数{ratio}のとき、母集団の相関係数の{(1-alpha)*100}%信頼区間は、{round(lo6_95,2)}~{round(up6_95,2)}')
標本数6で相関係数0.85のとき、母集団の相関係数の95.0%信頼区間は、0.12~0.98 標本数50で相関係数0.85のとき、母集団の相関係数の95.0%信頼区間は、0.75~0.91 標本数6で相関係数0.81のとき、母集団の相関係数の95.0%信頼区間は、-0.0~0.98
p219 相関は因果関係を保証しない
import pandas as pd
import math
from scipy import stats
# 設例データ
tall = [120,130,135,140,150,160,165,170,175,180]
mathematics = [13,28,35,60,55,72,90,80,84,83]
alpha = 1-0.95 # 信頼確率95%
# リストを Seriesに変換
s_tall = pd.Series(tall)
s_math = pd.Series(mathematics)
# 標本の相関係数を計算
res = s_tall.corr(s_math)
print(f'標本の相関係数:{round(res,3)}')
# 関数 集団の相関係数の信頼区間
def Conf_int(alpha, num, res): # 信頼確率、標本数、標本の相関係数
zvalue = (math.log((1+res)/(1-res)))/2 # フィッシャーのz変換
pvalue = stats.norm.ppf(1-alpha/2, loc=0) # p値
# 母集団の相関係数の下側
low = zvalue - pvalue * math.sqrt(1/(num-3))
Lower= (math.exp(2*low)-1)/(math.exp(2*low)+1)
# 母集団の相関係数の上側
up = zvalue + pvalue * math.sqrt(1/(num-3))
Upper= (math.exp(2*up)-1)/(math.exp(2*up)+1)
return [Lower, Upper]
# 集団の相関係数を計算
Lower = Conf_int(alpha, len(tall),res)[0]
Upper = Conf_int(alpha, len(tall),res)[1]
print(f'母集団の相関係数の {(1-alpha)*100}%区間推定:{round(Lower,3)}~{round(Upper,3)}')
# DF化
DF = pd.DataFrame([tall,mathematics]).T
DF.columns=['tall','mathematics']
DF
標本の相関係数:0.946 母集団の相関係数の 95.0%区間推定:0.783~0.987 tall mathematics 0 120 13 1 130 28 2 135 35 3 140 60 4 150 55 5 160 72 6 165 90 7 170 80 8 175 84 9 180 83
p220 相関は因果関係を保証しない(身長160cm以上に限定)
# コードは上記の続き
# 特定の身長以上の列を抽出
limit = 160
DF_limit = DF[DF['tall'] >= limit]
# 標本の相関係数を求める
limit_tall = pd.Series(DF_limit['tall'])
limit_math = pd.Series(DF_limit['mathematics'])
res_limit = limit_tall.corr(limit_math)
print(f'身長{limit}cm以上の標本の相関係数:{round(res_limit,3)}')
# 集団の相関係数を計算
Lower = Conf_int(alpha, DF_limit.shape[0],res_limit)[0]
Upper = Conf_int(alpha, DF_limit.shape[0],res_limit)[1]
print(f'母集団の相関係数の {(1-alpha)*100}%区間推定:{round(Lower,3)}~{round(Upper,3)}')
DF_limit
身長160cm以上の標本の相関係数:0.385 母集団の相関係数の 95.0%区間推定:-0.753~0.946 tall mathematics 5 160 72 6 165 90 7 170 80 8 175 84 9 180 83
p223 直線で回帰する 表7.8
import pandas as pd
import math
# 設例データ
year = [1985,1990,1995,1997,1999,2001]
Drowning_Deaths = [2004,1479,1214,1243,1179,1058]
# 相関係数
year_s = pd.Series(year)
DD_s = pd.Series(Drowning_Deaths)
res = year_s.corr(DD_s)
print(f'相関係数:{round(res,3)}')
# DF化
DF = pd.DataFrame([year,Drowning_Deaths]).T
DF.columns=['Year','Drowning_Deaths']
DF
相関係数:-0.954 Year Drowning_Deaths 0 1985 2004 1 1990 1479 2 1995 1214 3 1997 1243 4 1999 1179 5 2001 1058
p223 直線で回帰する 図7.6
# コードは上記の続き
from matplotlib import pyplot as plt
plt.plot(year,Drowning_Deaths)
plt.xlabel('Year')
plt.ylabel('Drowning_Deaths')
plt.xlim(1984,2002)
plt.ylim(800,2100)
plt.show()
p228 回帰直線 表7.9
# コードは上記の続き
DF['x'] = DF['Year']-1980
DF['y'] = DF['Drowning_Deaths']-1000
DF['xy'] = DF['x']*DF['y']
DF['x^2'] = DF['x']**2
DF.loc['Sum'] = DF.sum()
# 傾き a
angle = (DF['xy']['Sum']-DF['x']['Sum']*DF['y']['Sum']/len(year))/(DF['x^2']['Sum']-DF['x']['Sum']**2/len(year))
print(f'傾き a:{round(angle,2)}')
# 切片 b
intercept_b = DF['Drowning_Deaths']['Sum']/len(year) - round(angle,1) *DF['Year']['Sum']/len(year)
print(f'切片 b:{round(intercept_b,2)}')
DF
傾き a:-54.58 切片 b:110262.53 Year Drowning_Deaths x y xy x^2 0 1985 2004 5 1004 5020 25 1 1990 1479 10 479 4790 100 2 1995 1214 15 214 3210 225 3 1997 1243 17 243 4131 289 4 1999 1179 19 179 3401 361 5 2001 1058 21 58 1218 441 Sum 11967 8177 87 2177 21770 1441
p228 回帰直線 グラフ
# コードは上記の続き plt.scatter(year,Drowning_Deaths) x_s = [] y_s = [] for i in range(1980,2012): x_s.append(i) y_s.append(i*angle+intercept_b) plt.plot(x_s,y_s) plt.xlim(1984,2012) plt.ylim(400,2200)