「統計解析のはなし―データに語らせるテクニック」5章~6章
大村平「統計解析のはなし―データに語らせるテクニック」日科技連 の読後行間補充メモ
同書籍は、印刷数表と手計算による統計解析を紹介した良書。
本稿では、同書籍の設例について、プログラムによる演算処理をした場合の例を示す。
コードと出力例は、Python[Google Colaboratory]
5章 代表選手の言い分を聞く
p138 e の -m乗 の一覧表
import pandas as pd
import math
mlist = pd.DataFrame([0,0.01,0.02,0.05,0.1,0.2,0.3,0.5,1,2,3,5,8])
e_list = round(math.e**(-mlist),5)
emlist = pd.DataFrame(e_list)
DF = pd.concat([mlist,emlist],axis=1)
DF.columns=['m','e^{-m}']
DF
m e^{-m}
0 0.00 1.00000
1 0.01 0.99005
2 0.02 0.98020
3 0.05 0.95123
4 0.10 0.90484
5 0.20 0.81873
6 0.30 0.74082
7 0.50 0.60653
8 1.00 0.36788
9 2.00 0.13534
10 3.00 0.04979
11 5.00 0.00674
12 8.00 0.00034
p139 ロット不良品率、標本数、標本中の不良品数 → そのようになる確率
母集団が大きく(例:1ロットあたり数千個)、ロット不良率が小さく( \(p<0.1\) )、標本数(サンプル数)が一定数以上(\(n>50\))等の前提での近似式(ポアソン分布)を使用。
import math
p = float(input('ロットの不良品率:',))
n = int(input('標本の数:',))
r = int(input('標本中の不良品数:',))
P_r = (n*p)**r/math.factorial(r)*(math.e)**(-n*p)
print(f'上記のようになる確率:{round(P_r,3)}')
ロットの不良品率:0.01 標本の数:50 標本中の不良品数:1 上記のようになる確率:0.303
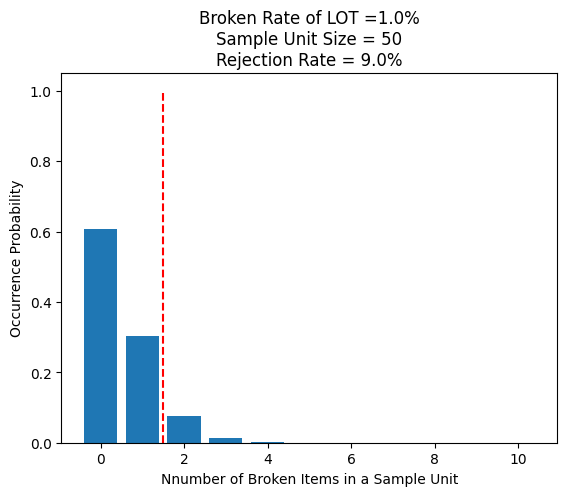
p140 ロットが合格する確率(サンプル50個中に不良品1個以下ならロット合格との検査基準)
import math
BRL = float(input('ロットの不良品率:',))
snumber = int(input('標本の数:',))
xrange = range(0, 11) # グラフ化する横軸上限
NBI = []
OBRL = []
for r in xrange:
NBI.append(r) # 標本中の不良品数
P = (snumber*BRL)**r/math.factorial(r)*(math.e)**(-snumber*BRL)
OBRL.append(P) # 確率
accept_rate = OBRL[0]+OBRL[1] # 合格になる率
reject_rate = round(1-accept_rate,3) # 不合格になる率
plt.bar(NBI, OBRL)
plt.title(f"Broken Rate of LOT ={BRL*100}%\nSample Unit Size = {snumber}\nRejection Rate = {reject_rate*100}%")
plt.xlabel(f"Nnumber of Broken Items in a Sample Unit")
plt.ylabel("Occurrence Probability")
plt.vlines(1.5,0,1, colors='red', linestyle='dashed') # 合格ライン
plt.show()
p142 図5.2 OC曲線
検査基準(ロットから抽出した50個の標本中における不良品が1個以下ならロット合格とする基準)を前提とした \(x\) 軸(ロットの真実の不良率)と \(y\) 軸(ロットが同検査基準で合格する確率)の関係
import math
import matplotlib.pyplot as plt
snumber = int(input('標本の数:',))
permissable = int(input('標本中の許容不良品個数:',))
LOT_P = [] # ロット中の不良率の配列
Series_LPR = []
for lotp in range(0, 200, 1):
prob = lotp/1000 # 0~0.2 の数値(演算用)
LOT_P.append(lotp/10) # 0~20 の数値をx軸データとして格納(%表記用)
Ps = []
rs = range(0, snumber) # 標本中の不良品個数
for r in rs:
# snumber個の標本中にr個だけ不良品が含まれる確率
Probability = (snumber*prob)**r/math.factorial(r)*(math.e)**(-snumber*prob)
Ps.append(Probability) # 各確率のリスト
Lot_Pass_Rate = 0
for pm in range(0,permissable+1):
Lot_Pass_Rate += Ps[pm]*100 # 許容不良品個数までの全確率を合計
Series_LPR.append(Lot_Pass_Rate) # y軸用データ
plt.plot(LOT_P, Series_LPR)
plt.xlim(0,13)
plt.ylim(0,)
plt.grid()
plt.title(f"OC curve\nSample Size = {snumber}\nNumber of defective products allowed = {permissable}")
plt.xlabel('Lot Defective Rate [%]')
plt.ylabel('Lot Pass Rate [%]')
plt.show()
p144 図5.3 OC曲線
検査基準(ロットから抽出した50個の標本中における不良品が0個、1個以下、2個以下ならロット合格とする基準)を前提とした \(x\) 軸(ロットの真実の不良率)と \(y\) 軸(ロットが同検査基準で合格する確率)の関係
import math
import matplotlib.pyplot as plt
# 設定数値
snumber = 50
# 関数 OC曲線
def OC_curve (snumber,permissable): # 標本数、許容不良品個数を引数
LOT_P = [] # x軸データ用
Series_LPR = [] #y軸データ用
for lotp in range(0, 200, 1):
prob = lotp/1000 # 0~0.2 の数値(演算用)
LOT_P.append(lotp/10) # 0~20 の数値(x軸要素)
rs = range(0, snumber) # 標本中の不良品の個数
Ps = []
for r in rs:
Probability = (snumber*prob)**r/math.factorial(r)*(math.e)**(-snumber*prob)
Ps.append(Probability) # 各確率のリスト
Lot_Pass_Rate = 0
for pm in range(0,permissable+1):
Lot_Pass_Rate += Ps[pm]*100 # 許容不良品個数までの全確率を合計
Series_LPR.append(Lot_Pass_Rate)
return [LOT_P,Series_LPR] # x軸データ、y軸データが戻り値
# 許容不良品個数0~2のグラフ用データを関数で計算して取得
LDR, LPR_0 = OC_curve(snumber,0)
LDR, LPR_1 = OC_curve(snumber,1)
LDR, LPR_2 = OC_curve(snumber,2)
#グラフを表示する領域を,figオブジェクトとして作成.
fig = plt.figure(figsize = (6,4), facecolor='lightblue')
# グラフを描画
plt.plot(LDR, LPR_0, color='blue', label="Criteria =0")
plt.plot(LDR, LPR_1, color='green', label="Criteria ~1")
plt.plot(LDR, LPR_2, color='red', label="Criteria ~2")
plt.xlim(0,13)
plt.ylim(0,)
plt.title(f"OC curve, Sample Unit Size = {snumber}")
plt.xlabel("Defective Product Rate in Lot")
plt.ylabel("Lot Pass Rate")
plt.legend(loc = 'upper right')
plt.show()
p144 図5.4 OC曲線
検査基準(ロットから抽出した標本中における不良品が2%以下ならロット合格とする基準)を前提とした \(x\) 軸(ロットの真実の不良率)と \(y\) 軸(ロットが同検査基準で合格する確率)の関係
def OC_curve_n (snumber):
LOT_P = []
Series_LPR = []
permissable = int(snumber/50) # 標本数の1/50 =2% →許容不良品個数
for lotp in range(0, 200, 1):
prob = lotp/1000 # 0~0.2 の数値
LOT_P.append(lotp/10) # 0~20 の数値をx軸要素として格納
rs = range(0, snumber) # 標本中の不良品の個数
Ps = []
for r in rs:
Rs.append(r)
Probability = (snumber*prob)**r/math.factorial(r)*(math.e)**(-snumber*prob)
Ps.append(Probability)
Lot_Pass_Rate = 0
for pm in range(0,permissable+1):
Lot_Pass_Rate += Ps[pm]*100
Series_LPR.append(Lot_Pass_Rate)
return [LOT_P,Series_LPR]
LDR, LPR_050 = OC_curve_n(50)
LDR, LPR_100 = OC_curve_n(100)
LDR, LPR_150 = OC_curve_n(150)
#グラフを表示
fig = plt.figure(figsize = (6,4), facecolor='lightgrey')
plt.plot(LDR, LPR_050, color='green', label='~1 in 50')
plt.plot(LDR, LPR_100, color='blue', label='~2 in 100')
plt.plot(LDR, LPR_150, color='red', label='~3 in 150')
plt.title(f"OC curve, Allowable Rate = 2%")
plt.xlim(0,13)
plt.ylim(0,)
plt.xlabel(xl1)
plt.ylabel(yl1)
plt.legend(loc = 'upper right')
plt.show()
p151 表5.2 JIS Z 9002
同表の \(p_0 = 0.901~1.12\)% に記載の抜取個数 \(n\) と合格判定基準数 \(c\) に対応する生産者リスク \(\alpha\) と消費者リスク \(\beta\) を試算。必ずしも、\(\alpha=5\)% 、消費者リスク \(\beta=10\)% 以内とはなっていない。
import pandas as pd
import math
from decimal import Decimal
# 数表データ
p1col = pd.DataFrame([3.55,4.50,5.6,7.1,9,11.2,14]) # p1上限
p1col_under = pd.DataFrame([2.81,3.56,4.51,5.61,7.11,9.01,11.3]) # p1下限
p0901n = pd.DataFrame([300,200,120,80,60,40,30])
p0901c = pd.DataFrame([6,4,3,2,2,1,1])
DF_p0901 = pd.concat([p1col, p1col_under, p0901n, p0901c], axis=1).T
DF_p0901.index = ['不合格ロット水準 p1[%]上限','不合格ロット水準 p1[%]下限','抜取個数 s','合格判定個数 c']
# 関数(ロット不良品率、標本数、許容不良品数)→ロット合格率、不合格率
def RiskRate(prob_per, snumber, allowed):
prob = prob_per/100 # 演算用
defective = range(0, snumber)
Probs = []
for defect in defective:
Probability = Decimal((snumber*prob)**defect)/Decimal(math.factorial(defect))*Decimal((math.e)**(-snumber*prob))
Probs.append(float(Probability))
Lot_Pass_Rate = 0
for pm in range(0,allowed+1):
Lot_Pass_Rate += Probs[pm]
return round(Lot_Pass_Rate,2), round(1-Lot_Pass_Rate,2)
# 生産者リスク上限の行を追加
supplier_risk = []
for i in DF_p0901.columns:
supplier_risk.append(RiskRate(1.12,int(DF_p0901[i][2]),int(DF_p0901[i][3]))[1])
DF_p0901.loc["生産者risk(上限)"] = supplier_risk
# 生産者リスク下限の行を追加
supplier_risk = []
for i in DF_p0901.columns:
supplier_risk.append(RiskRate(0.901,int(DF_p0901[i][2]),int(DF_p0901[i][3]))[1])
DF_p0901.loc["生産者risk(下限)"] = supplier_risk
# 消費者リスク上限の行を追加
user_risk = []
for j in DF_p0901.columns:
user_risk.append(RiskRate(DF_p0901[j][1],int(DF_p0901[j][2]),int(DF_p0901[j][3]))[0])
DF_p0901.loc["消費者risk(上限)"] = user_risk
# 消費者リスク下限の行を追加
user_risk = []
for j in DF_p0901.columns:
user_risk.append(RiskRate(DF_p0901[j][0],int(DF_p0901[j][2]),int(DF_p0901[j][3]))[0])
DF_p0901.loc["消費者risk(下限)"] = user_risk
DF_p0901
p154 表5.6 AOQ 曲線
不合格となったロットは全数検査をして全品を良品としてから出荷する場合の出荷商品不良率(\(pP\))曲線(\(AOQ\) 曲線)。\(AOQ\) 曲線 の目盛は、\(OC\) 曲線に同じ。但し、視認性向上のため、 \(AOQ\) 曲線を縦軸10倍表記した。
import math
import matplotlib.pyplot as plt
# 関数 OC曲線
def OC_curve (number, permissable): # サンプル数、許容不良品数
LOT_P = []
Series_LPR = []
for lotp in range(0, 200, 1):
prob = lotp/1000 # 0~0.2 の数値(演算用)
LOT_P.append(lotp/10) # 0~20 の数値(x軸要素)
rs = range(0, number) # for 文の繰返しリスト
Ps = []
for r in rs:
Posibility = (number*prob)**r/math.factorial(r)*(math.e)**(-number*prob)
Ps.append(Posibility) # 確率
Lot_Pass_Rate = 0
for pm in range(0,permissable+1):
Lot_Pass_Rate += Ps[pm]*100 # 確率を許容不良品数分まで合算
Series_LPR.append(Lot_Pass_Rate) # ロット不良率ごとの確率和をリスト化
return [LOT_P,Series_LPR] # OC曲線のx、yデータ
# 設定数値
number = 50 # 標本の数
permissable =1 # 許容不良品数
# 演算→グラフ用データ
LDR, LPR = OC_curve(number, permissable) # x,yデータを演算し取得
AOQ = [x * y/10 for (x, y) in zip(LDR, LPR)] #リスト要素を掛け算
### 複数のグラフを重ねて表示
fig = plt.figure(figsize = (6,4), facecolor='lightblue')
plt.plot(LDR, LPR, color='blue', label='OC', linestyle = "dashed")
plt.plot(LDR, AOQ, color='green', label='AOQ*10') #AOQ表記10倍
plt.xlim(0,12)
plt.ylim(0,)
plt.title(f"OC curve, AOQ")
plt.xlabel('Defective Product Rate in Lot [%]')
plt.ylabel('Lot Pass Rate [%]')
plt.legend(loc = 'upper right')
plt.show()
p158 図5.7 2回抜取検査の効果
import math
import matplotlib.pyplot as plt
# 設定
snumber = 50 # 標本の数
# 関数 2回抜取検査での合格率
def P2(n,p): # 標本数、ロット不良率
return (math.e)**(-n*p) +n*p*(math.e)**(-n*p)*(math.e)**(-n*p)
del n,p
# 関数 2回抜取検査の曲線
def P2_curve(n): # 標本数
LOT_P = []
Series_LPR = []
Ps = []
for lotp in range(0, 200, 1):
p = lotp/1000 # 0~0.2 の数値
LOT_P.append(lotp/10) # 0~20 の数値(x軸要素)
P2value = P2(n,p)*100 # 関数(2回抜取検査での合格率)
Ps.append(P2value) # ロット不良率ごとの合格率リスト
return [LOT_P,Ps] # 2回抜取検査の曲線データ
del n
# 関数 OC曲線
def OC_curve (n, permissable): # 標本数、標本中の許容不良品個数
LOT_P = []
Series_LPR = []
for lotp in range(0, 200, 1):
p = lotp/1000 # 0~0.2 の数値(演算用)
LOT_P.append(lotp/10) # 0~20 の数値(x軸要素)
rs = range(0, n)
Ps = []
for r in rs:
P = (n*p)**r/math.factorial(r)*(math.e)**(-n*p) # ポアソン分布
Ps.append(P)
Lot_Pass_Rate = 0
for pm in range(0,permissable+1):
Lot_Pass_Rate += Ps[pm]*100
Series_LPR.append(Lot_Pass_Rate)
return [LOT_P,Series_LPR] # OC曲線データ
del n, permissable
# 関数の呼出し
LDR, LPR_0 = OC_curve(snumber,0) # 許容不良品個数0 条件での x,y データ取得
LDR, LPR_1 = OC_curve(snumber,1) # 許容不良品個数0 条件での x,y データ取得
LDR, LPR_2 = P2_curve(snumber) # 2回抜取検査での x,y データ取得
# 複数のグラフを重ねて表示
fig = plt.figure(figsize = (6,4), facecolor='lightblue')
x_ax = LDR # x 軸は共用
plt.plot(x_ax, LPR_0, color='blue', label='Detective =0', linestyle='dashed')
plt.plot(x_ax, LPR_1, color='green', label='Detective ~1', linestyle='dashed')
plt.plot(x_ax, LPR_2, color='red', label='Double Sampling Inspection')
plt.xlim(0,12)
plt.ylim(0,)
plt.title(f"OC curve, sample unit size = {snumber}")
plt.xlabel('Defective Product Rate in Lot')
plt.ylabel('Lot Pass Rate')
plt.legend(loc = 'upper right')
plt.show()
p158 図5.8 2回抜取検査の AOQ 曲線
AOQ = [x * y/100 for (x, y) in zip(LDR, LPR_2)] #リスト要素を掛け算
#グラフを表示
fig = plt.figure(figsize = (6,4), facecolor='lightblue')
plt.xlim(0,12)
plt.ylim(0,1.2)
plt.grid()
plt.plot(LDR, AOQ, color='blue', label='AOQ')
plt.title(f"AOQ")
plt.xlabel('Defective Product Rate in Lot [%]')
plt.ylabel('Lot Pass Rate [%]')
plt.legend(loc = 'upper right')
plt.show()
p159 超幾何分布
import math
import pandas as pd
# 設定数値
N =10 # 母集団の個数
n = 8 # 標本数
r = 0 # 標本中の不良品数
# 関数 超幾何分布(hypergeometric distribution)
def HGD(N,k,n,r):
return math.comb(k,r)*math.comb(N-k,n-r)/math.comb(N,n)
k_values = [] # 母集団の不良品個数のリスト
p_values = [] # 母集団の不良率のリスト
Prob_values = [] # 合格確率のリスト
for k in range(0,N+1): # 全てのkについて
k_values.append(k) # 母集団中の故障品数 k列を作成
p_values.append(k/N) # 母集団中の故障品比率 p列を作成
Prob_values.append(HGD(N,k,n,r)) # 確率 P列を作成
DF = pd.DataFrame([k_values,p_values,Prob_values],
index=['k_value','p_value','Probability']).T
answer = 1/DF['Probability'].sum() # ベイズの定理
print(f'母集団の不良品率が0の確率:{round(answer*100,1)}%')
DF
6章 ばらつきをばらす法 分散分析のはなし
p172~180 列の効果と誤差とを分離する
→ 列効果、誤差を分離
→ 列効果と誤差との比率を算定
→ 同比率が偶然でも生じ得る水準か否かを希少性基準5%で \(F\) 検定
import pandas as pd
import matplotlib.pyplot as plt
from numpy import NaN
from scipy.stats import f
# 設定データ
index_info = ['1st','2nd','3rd']
columns_info = ['Raven','Summer','Cinder','Winter']
DF = pd.DataFrame([
[136,107,136,113],
[129,104,NaN,108],
[128,NaN,127,112]
],index = index_info, columns = columns_info)
# DFの概要
Total = DF.sum().sum() #全要素の合計
Number = DF.size #全要素の数
NaNs = DF.isnull().sum() #NaNの個数状況
Fignum = Number - NaNs.sum() #数値がある要素数
Total_average = Total/Fignum #数値の平均値
# DFの加工
DF.loc['Sum'] = DF.sum() #縦合計を新行で追加
DF.loc['Mean'] = DF.iloc[0:3].mean() #0-2行目までの平均を新行で追加
DF.loc['c_effect'] = DF.loc['Mean']-Total_average #列効果を新行で追加
# 誤差データDF、誤差の不偏分散V1
DF_diff = DF.iloc[0:3]-DF.loc['Mean'] #誤差 各要素から列平均値を引く
Number2 = DF_diff.size #全要素の数
NaNs2 = DF_diff.isnull().sum() #NaNの個数状況
Fignum2 = Number2 - NaNs2.sum() #数値がある要素数
dof = Fignum2-4 # 自由度
DF_2 = (DF_diff-0)**2 #全要素を二乗
Numerator = DF_2.sum().sum() #二乗値の合計
V1 = Numerator/dof # 誤差の不偏分散V1
print(f'誤差の不偏分散V1:{round(V1,1)}')
# 列の効果DF
## 列の効果リスト
columns_effect = DF.loc['c_effect'] #列の効果リスト
DF_66a =pd.DataFrame(columns_effect).T
DF_66a_2 = columns_effect**2 #全要素を二乗
## データの個数DF
columns_datasize = []
for i in NaNs2:
j = DF_diff.shape[0] - i #行数(列にある全データ数)-NaN個数
columns_datasize.append(j)
DF_66b = pd.DataFrame(columns_datasize).T
## 列の効果の不偏分散V2
Numerator66_list = [x * y for x, y in zip(DF_66a_2,columns_datasize )] #列効果^2 × データ数
dof2 = len(columns_effect)-1 # V2の自由度
V2 = sum(Numerator66_list)/dof2 # 列の効果 の不偏分散V2
print(f'列の効果の不偏分散V2:{round(V2,1)}')
# F検定
## 列の効果の不偏分散V2 / 誤差の不偏分散V1
F_value = round(V2,1)/round(V1,1) # 本件のF値
dfn = dof2 # V1の自由度
dfd = dof # V2の自由度
percent_value = f.sf(F_value, dfn, dfd, loc=0, scale=1)*100
print(f'本件のF値:{round(F_value,2)}, その確率:{round(percent_value,2)}%')
## 基準値:危険率5%(累積確率95%)
F005 = f.ppf(0.95, dfn, dfd, loc=0, scale=1)
percent_005 = f.sf(F005, dfn, dfd, loc=0, scale=1)*100
print(f'基準のF値:{round(F005,2)}, その確率:{round(percent_005,2)}%')
## 検定
if percent_value > percent_005:
print('仮説「列の効果は無し」は、未棄却')
else:
print('仮説「列の効果は無し」は、棄却')
# 列の効果DF
DF_66b.columns = columns_info
DF_66b.index=['Datasize']
DF66 = pd.concat([DF_66a, DF_66b],axis=0,ignore_index=False) #表6.6
print(f'\n表6.4上段\n{DF}')
print(f'\n表6.4下段\n{DF_diff}')
print(f'\n表6.6\n{DF66}')
p180~185 因子が2つの場合
- 知能テストの種類による判定有意差(行効果)があるか。
- 4名の知能指数に有意差(列効果)があるか。
→ 行効果、列効果、誤差を分離し、各効果と誤差との比率を基準5%で \(F\) 検定
from numpy import NaN
import pandas as pd
from matplotlib import pyplot as plt
from scipy.stats import f
# 設例
index_type =['Test_A','Test_B','Test_C']
DF = pd.DataFrame([
[133,97,143,115],
[126,106,120,109],
[131,100,136,112]
],index=index_type ,columns=['Ruby','Yang','Blake','Weiss'])
# DF概要
test_valuation = DF.shape[0] # テスト種別の数
Total = DF.sum().sum() #全要素の合計
Number = DF.size #全要素の数
NaNs = DF.isnull().sum() #NaNの個数状況
Fignum = Number - NaNs.sum() #数値がある要素数
Total_average = Total/Fignum #数値の平均値
# 行を追加(縦合計、縦平均、列効果)
DF.loc['Sum'] = DF.sum() #縦合計を新行で追加
DF.loc['Mean'] = DF.iloc[0:3].mean() #0-2行目までの平均を新行で追加
DF.loc['column_effect'] = DF.loc['Mean']-Total_average #列平均値[Mean]と全体平均値との差を新行で追加
# 列を追加(横合計、横平均、行効果)
R_sum = DF[0:test_valuation].sum(axis=1) # 点数の横合計を各行について計算
R_sum_column = pd.DataFrame(R_sum, columns = ['row_sum']) # DF化
R_mean = DF[0:test_valuation].mean(axis=1) # 点数の横平均
rMean_column = pd.DataFrame(R_mean, columns = ['row_mean']) # DF化
DF2 = pd.concat([R_sum_column, rMean_column], axis=1) # DF化
DF2['row_effect'] = DF2['row_mean']-Total_average #行効果を新列で追加
# 表6.7
DF_wide = pd.concat([DF, DF2], axis=1) # DFと新列DFとを統合
# 誤差 表6,8
DF_diff = DF.iloc[0:3]-Total_average -DF.loc['column_effect'] #各要素から平均値と行要素を引く
for m in range(3):
DF_diff.iloc[m] = DF_diff.iloc[m]-DF_wide['row_effect'][m] #各要素から列要素を引く
# 誤差の自由度
rows_columns = DF_diff.shape # 行数と列数
dof = (rows_columns[0]-1)*(rows_columns[1]-1) # 自由度の公式 p183
# 誤差の不偏分散 V1
DF_2 = (DF_diff-0)**2 #全要素を二乗
Numerator = DF_2.sum().sum() #二乗値の合計
V1 = Numerator/dof
# 行の効果の不偏分散 V2
V2_nume =0
r_effect = DF2['row_effect']
for r_e in r_effect: #行効果の数値を取り出す
V2_nume += (r_e**2)*rows_columns[1] #分子
V2_deno = rows_columns[0]-1 #分母
V2 = V2_nume/V2_deno
# 列の効果の不偏分散 V3
V3_nume =0
for c_e in DF.loc['column_effect']: #列効果の数値を取り出す
V3_nume += (c_e**2)*rows_columns[0] #分子
V3_deno = rows_columns[1]-1 #分母
V3 = V3_nume/V3_deno
# 行の効果にかかるF検定
F_row = V2/V1
dfn = V2_deno #F値の上数値(=行効果の自由度)
dfd = dof #F値の下数値(=誤差の自由度)
row_percent = f.sf(F_row, dfn, dfd, loc=0, scale=1)*100
# 列の効果にかかるF検定
F_col = V3/V1
# →上側確率
dfn = V3_deno #F値の上数値(=列効果の自由度)
dfd = dof #F値の下数値(=誤差の自由度)
col_percent = f.sf(F_col, dfn, dfd, loc=0, scale=1)*100
# 平均値、不偏分散の表示
print(f'平均値:{Total_average}')
print(f'誤差の不偏分散 V1: {round(V1,2)}')
print(f'行の効果の不偏分散 V2: {round(V2,2)}')
print(f'列の効果の不偏分散 V3: {round(V3,2)}')
# 行の効果の判定を表示
print(f'\n行の効果のF値:{round(F_row,2)}, その確率:{round(row_percent,2)}%')
if row_percent>5:
print('行の効果なし(テスト種類による有意差なし)')
else:
print('行の効果あり(テスト種類による有意差あり)')
# 列の効果の判定を表示
print(f'\n列の効果のF値:{round(F_col,2)}, その確率:{round(col_percent,2)}%')
if col_percent>5:
print('列の効果なし(個人間の知能指数に有意差なし)')
else:
print('列の効果あり(個人間の知能指数に有意差あり)')
# 数表の表示
print(f'\n表6.7\n{DF_wide}')
print(f'\n表6.8\n{DF_diff}')
p185 因子が3つの場合(観測データ)
- 2種類の知能テストの種類による判定有意差(行効果)があるか。
- 2名の知能指数に有意差(列効果)があるか。
- 午前と午後のテストで知能指数に有意差(層効果)があるか。
→ 行効果、列効果、層効果、誤差を分離し、各効果と誤差との比率を基準5%で \(F\) 検定
import numpy as np
import pandas as pd
from scipy.stats import f
# 第1層
index_type =['1st_row','2nd_row'] # 各層で共用
columns_type = ['1st_col','2nd_col'] # 各層で共用
DF1 = pd.DataFrame([
[124,107],
[100,85],
],index= index_type, columns =columns_type)
# 第2層
DF2 = pd.DataFrame([
[116,99],
[93,76]
],index= index_type, columns =columns_type)
print(f'1層{DF1}')
print(f'\n2層{DF2}')
Total = DF1.sum().sum()+DF2.sum().sum() #全要素の合計
Number = DF1.size + DF2.size #全要素の数
NaNs = DF1.isnull().sum()+DF2.isnull().sum() #NaNの個数状況
Fignum = Number - NaNs.sum() #数値がある要素数
Total_average = Total/Fignum #数値の平均値
print(f'\n全要素の合計値:{Total}\n平均値:{Total_average}')
1層 1st_col 2nd_col 1st_row 124 107 2nd_row 100 85 2層 1st_col 2nd_col 1st_row 116 99 2nd_row 93 76 全要素の合計値:800 平均値:100.0
p188 因子が3つの場合(表6.9 列の情報の一覧表)
# コードは上記の続き
col_sum = DF1.sum()+DF2.sum() # 各列の合計
col_num = DF1.shape[0]+DF2.shape[0] #列の要素数(=行数)
col_ave = col_sum/col_num # 各列の平均
col_effect = col_ave - Total_average # 列の効果
index_c =['c_sum','c_average','c_effect']
columns_c = ['1st_col','2nd_col']
col_info = pd.DataFrame([col_sum,col_ave,col_effect],
index= index_c, columns =columns_c)
col_info
1st_col 2nd_col c_sum 433.00 367.00 c_average 108.25 91.75 c_effect 8.25 -8.25
p188 因子が3つの場合(表6.9 行の情報の一覧表)
# コードは上記の続き
test_variation = DF1.shape[0] # 行数(DF1,DF2共通)
R_sum1 = [DF1[0:test_variation].sum(axis=1)][0] # 第1層の点数の横合計
R_sum2 = [DF2[0:test_variation].sum(axis=1)][0] # 第2層の点数の横合計
row1_sum = R_sum1[0]+R_sum2[0] #両層の1行目の合計
row2_sum = R_sum1[1]+R_sum2[1] #両層の2行目の合計
row1_ave = row1_sum/4 #1行目の平均
row2_ave = row2_sum/4 #2行目の平均
r1_effect = row1_ave - Total_average #1行目の効果
r2_effect = row2_ave - Total_average #2行目の効果
# 行の情報の一覧表
index_r =['r_sum','r_average','r_effect']
columns_r = ['1st_row','2nd_row']
row_info = pd.DataFrame([
[row1_sum,row2_sum], [row1_ave,row2_ave], [r1_effect,r2_effect]],
index= index_r, columns =columns_r)
row_info.T
r_sum r_average r_effect 1st_row 446.0 111.5 11.5 2nd_row 354.0 88.5 -11.5
p188 因子が3つの場合(表6.9 層の情報の一覧表)
# コードは上記の続き l_sum = pd.DataFrame([DF1.sum().sum(),DF2.sum().sum()]) #要素の合計値 l_ave = pd.DataFrame([DF1.sum().sum()/DF1.size,DF2.sum().sum()/DF2.size]) #要素の平均値 l_effect = l_ave -Total_average index_l =['r_sum','r_average','r_effect'] columns_l = ['1st_level','2nd_level'] level_info = pd.concat([l_sum,l_ave,l_effect],axis=1) level_info.index=['1st_level','2nd_level'] level_info.columns=['l_sum','l_average','l_effect'] level_info
l_sum l_average l_effect 1st_level 416 104.0 4.0 2nd_level 384 96.0 -4.0
p188 因子が3つの場合(表6.11 誤差)
# コードは上記の続き # 1層目の誤差 DF_diff_1L = DF1-Total_average -col_info.loc['c_effect']-level_info['l_effect'][0] #平均、列効果、層効果を除去 DF_diff_1L.loc['1st_row'] = DF_diff_1L.loc['1st_row']-r1_effect #1目行効果を除去 DF_diff_1L.loc['2nd_row'] = DF_diff_1L.loc['2nd_row']-r2_effect #2行目効果を除去 print(DF_diff_1L) # 2層目の誤差 DF_diff_2L = DF2-Total_average -col_info.loc['c_effect']-level_info['l_effect'][1] #平均、列効果、層効果を除去 DF_diff_2L.loc['1st_row'] = DF_diff_2L.loc['1st_row']-r1_effect #1目行効果を除去 DF_diff_2L.loc['2nd_row'] = DF_diff_2L.loc['2nd_row']-r2_effect #2行目効果を除去 print(DF_diff_2L)
1st_col 2nd_col
1st_row 0.25 -0.25
2nd_row -0.75 0.75
1st_col 2nd_col
1st_row 0.25 -0.25
2nd_row 0.25 -0.25
p189~190 因子が3つの場合(不偏分散[誤差、行の効果、列の効果、層の効果])
# コードは上記の続き
# 誤差の不偏分散 V1
DF1L = (DF_diff_1L-0)**2 #全要素を二乗(1層目)
DF2L = (DF_diff_2L-0)**2 #全要素を二乗(1層目)
Numerator_e = DF1L.sum().sum()+DF2L.sum().sum() #二乗値の合計
dof_e = 4
V1 = Numerator_e/dof_e
print(f'誤差の不偏分散 V1:{V1}')
# 行の効果の不偏分散 V2
Numerator_r = r1_effect**2*4+r2_effect**2*4
dof_r = 2-1
V2 = Numerator_r/dof_r
print(f'行の効果の不偏分散 V2:{V2}')
# 列の効果の不偏分散 V3
Numerator_c = col_effect[0]**2*4+col_effect[1]**2*4
dof_c = 2-1
V3 = Numerator_c/dof_c
print(f'列の効果の不偏分散 V3:{V3}')
# 層の効果の不偏分散 V4
Numerator_l = l_effect[0][0]**2*4 +l_effect[0][1]**2*4
dof_l = 2-1
V4 = Numerator_l/dof_l
print(f'層の不偏分散 V4:{V4}')
誤差の不偏分散 V1:0.375 行の効果の不偏分散 V2:1058.0 列の効果の不偏分散 V3:544.5 層の不偏分散 V4:128.0
p189~190 因子が3つの場合(各効果のF検定)
# コードは上記の続き
## 行の効果にかかるF検定
F_row = V2/V1
dfn = dof_r #F値の上数値(=行効果の自由度)
dfd = dof_e #F値の下数値(=誤差の自由度)
percent = f.sf(F_row, dfn, dfd, loc=0, scale=1)*100 # 確率
if percent>5:
print(f'行の効果のF値:{round(F_row,1)} →その確率:{round(percent,4)}% →行の効果なし')
else:
print(f'行の効果のF値:{round(F_row,1)} →その確率:{round(percent,4)}% →行の効果あり')
del dfn, dfd, percent
## 列の効果にかかるF検定
F_col = V3/V1
dfn = dof_c #F値の上数値(=列効果の自由度)
dfd = dof_e #F値の下数値(=誤差の自由度)
percent = f.sf(F_col, dfn, dfd, loc=0, scale=1)*100 # 確率
if percent>5:
print(f'列の効果のF値:{round(F_col,1)} →その確率:{round(percent,4)}% →列の効果なし')
else:
print(f'列の効果のF値:{round(F_col,1)} →その確率:{round(percent,4)}% →列の効果あり')
del dfn, dfd, percent
## 層の効果にかかるF検定
F_level = V4/V1
dfn = dof_l #F値の上数値(=層効果の自由度)
dfd = dof_e #F値の下数値(=誤差の自由度)
percent = f.sf(F_row, dfn, dfd, loc=0, scale=1)*100 # 確率
if percent>5:
print(f'層の効果のF値:{round(F_level,1)} →その確率:{round(percent,4)}% →層の効果なし')
else:
print(f'層の効果のF値:{round(F_level,1)} →その確率:{round(percent,4)}% →層の効果あり')
行の効果のF値:2821.3 →その確率:0.0001% →行の効果あり 列の効果のF値:1452.0 →その確率:0.0003% →列の効果あり 層の効果のF値:341.3 →その確率:0.0001% →層の効果あり
p194 表6.13 ラテン格子(実験計画法) 設例
import numpy as np
import pandas as pd
from scipy.stats import f
# 設例 観測データ
index_type =['1st_row','2nd_row','3rd_row','4th_row']
columns_type = ['1st_col','2nd_col','3rd_col','4th_col']
DF = pd.DataFrame([
[83,119, 81, 90],
[96,112, 85,107],
[90,115,106,129],
[77,113, 98, 99]
],index= index_type, columns =columns_type)
# DF概要
lines = DF.shape[0] # 行数
columns = DF.shape[1] # 列数
Total = DF.sum().sum() #全要素の合計
Number = DF.size #全要素の数
NaNs = DF.isnull().sum() #NaNの個数状況
Fignum = Number - NaNs.sum() #数値がある要素数
Total_average = Total/Fignum #数値の平均値
# 行を追加(縦合計、縦平均、列効果)
DF.loc['Sum'] = DF.sum() #縦合計を新行で追加
DF.loc['Mean'] = DF.iloc[0:lines].mean() #0-3行目までの平均を新行で追加
DF.loc['column_effect'] = DF.loc['Mean']-Total_average #列平均値[Mean]と全体平均値との差を新行で追加
# 列を追加(横合計、横平均、行効果)
R_sum = DF[0:lines].sum(axis=1) # 点数の横合計を各行について計算
R_sum_column = pd.DataFrame(R_sum, columns = ['row_sum']) # DF化
R_mean = DF[0:lines].mean(axis=1) # 点数の横平均
rMean_column = pd.DataFrame(R_mean, columns = ['row_mean']) # DF化
DF2 = pd.concat([R_sum_column, rMean_column], axis=1) # DF化
DF2['row_effect'] = DF2['row_mean']-Total_average #行効果を新列で追加
# 表6.13
DF_wide = pd.concat([DF, DF2], axis=1) # DFと新列DFとを統合
DF_wide
p195 表6.14 ラテン格子(実験計画法) 第3因子の効果
# コードは上記の続き
# 第3因子の影響を受けた要素をリスト化する関数
def Third_effect(LineN):
effect_list= []
for effected in range(lines):
effect_list.append(DF.iloc[effected][-effected + LineN])
return effect_list
# DF化
Third_E = []
for LineN in range(lines):
Third_E.append(Third_effect(LineN)) # 関数でリストを作成
DF_TE = pd.DataFrame(Third_E, index = ['A','B','C','D'])
TE_means = DF_TE[0:lines].mean(axis=1) # 横平均を各行で計算
DF_M = pd.DataFrame(TE_means, columns = ['mean'])
DF_614 = pd.concat([DF_TE, DF_M],axis=1) # データを結合
DF_614['3rd_effect'] = DF_614['mean']-Total_average # 第3因子効果を新列で追加
DF_614 # 表6.14
p196 表6.15 ラテン格子(実験計画法) 誤差
# コードは上記の続き
#各要素から平均値と列効果を引く
DF_diff = DF.iloc[0:lines] -Total_average -DF.loc['column_effect']
## 各要素から行効果を引く
for lis in range(lines): # 各行について
DF_diff.iloc[lis] = DF_diff.iloc[lis]-DF_wide['row_effect'][lis]
del lis
## 第3因子の効果を該当セルから控除する
for lis in range(lines): # 各行について
for cols in range(columns): # 各列について
DF_diff.iloc[lis][-lis+cols] -= DF_614['3rd_effect'][cols]
DF_diff # 表6.15
p196~197 ラテン格子(実験計画法) 行の効果のF 検定
# コードは上記の続き
# 誤差の不偏分散 V1
Numerator = ((DF_diff -0)**2).sum().sum() # 平方和
level =4 # レベル数
dof_e = (level-1)*(level-2) # 公式p196
V1 = Numerator/dof_e
print(f'誤差の不偏分散 V1:{round(V1,2)}')
# 行の効果の不偏分散 V2
Numerator_r = ((DF_wide["row_effect"]**2) *columns).sum()
dof_r = columns -1
V2 = Numerator_r/dof_r
print(f'行の効果の不偏分散 V2:{round(V2,2)}')
# 行の効果にかかるF検定
F_row = V2/V1
dfn = dof_r # F値の上数値(=行効果の自由度)
dfd = dof_e # F値の下数値(=誤差の自由度)
percent = f.sf(F_row, dfn, dfd, loc=0, scale=1)*100 # 確率
if percent>5:
print(f'行の効果のF値:{round(F_row,2)} →その確率:{round(percent,4)}% →行の効果なし')
else:
print(f'行の効果のF値:{round(F_row,2)} →その確率:{round(percent,4)}% →行の効果あり')
誤差の不偏分散 V1:5.08 行の効果の不偏分散 V2:208.17 行の効果のF値:40.95 →その確率:0.0217% →行の効果あり